AI tutor
Full solution
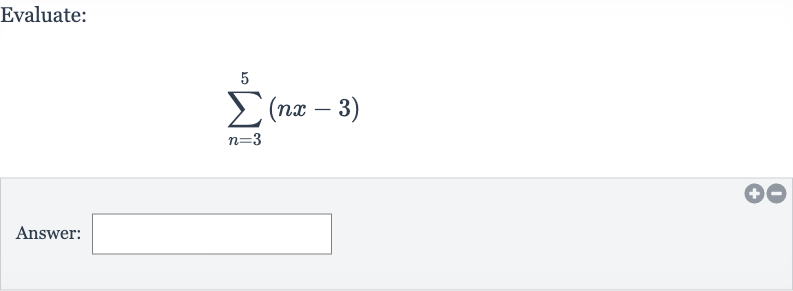
Q. Evaluate:Answer:
- Understand summation notation: Understand the summation notation. The expression means we need to evaluate for each integer value of from to and then sum the results.
- Evaluate for : Evaluate the expression for . Substitute into the expression to get .
- Evaluate for : Evaluate the expression for .Substitute into the expression to get .
- Evaluate for : Evaluate the expression for . Substitute into the expression to get .
- Add results from steps: Add the results from steps , , and . Sum the expressions: .
- Combine like terms: Combine like terms.Add the coefficients of and the constant terms separately: .
- Perform addition: Perform the addition.Calculate the sum of the coefficients of : .Calculate the sum of the constants: .
- Write final expression: Write the final expression.Combine the results from step to get the final expression: .
More problems from Evaluate rational expressions II
QuestionGet tutor help