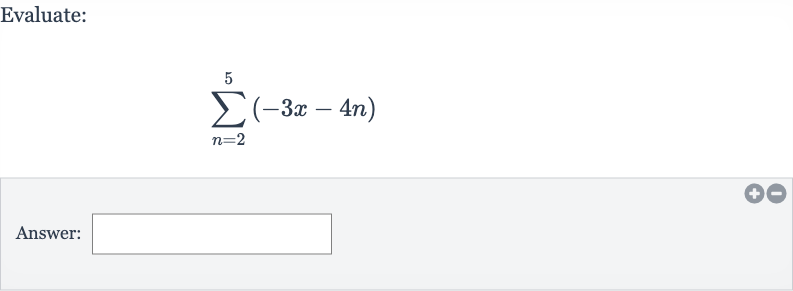
Evaluate: sum_(n=2)^(5)(-3x-4n) Answer:

Question

Evaluate:  sum_(n=2)^(5)(-3x-4n) Answer:

Bytelearn · Accepted Answer

Understand the problem: Understand the problem We need to evaluate the sum of the expression (-3x - 4n) for each integer value of n from 2 to 5.Write terms of sum: Write out the terms of the sum The sum is the addition of the expression (-3x - 4n) evaluated at n = 2, n = 3, n = 4, and n = 5.Evaluate n=2: Evaluate the expression for n = 2 Substitute n = 2 into the expression (-3x - 4n). (-3x - 4*2) = (-3x - 8)Evaluate n=3: Evaluate the expression for n = 3 Substitute n = 3 into the expression (-3x - 4n). (-3x - 4*3) = (-3x - 12)Evaluate n=4: Evaluate the expression for n = 4 Substitute n = 4 into the expression (-3x - 4n). (-3x - 4*4) = (-3x - 16)Evaluate n=5: Evaluate the expression for n = 5 Substitute n = 5 into the expression (-3x - 4n). (-3x - 4*5) = (-3x - 20)Add evaluated expressions: Add the evaluated expressions Add the results from steps 3 to 6. (-3x - 8) + (-3x - 12) + (-3x - 16) + (-3x - 20)Combine like terms: Combine like terms Combine the terms with x and the constant terms separately. (-3x - 3x - 3x - 3x) + (-8 - 12 - 16 - 20) (-12x) + (-56)Simplify expression: Simplify the expression Simplify the sum to get the final answer. -12x - 56

Evaluate: $\newline$ $\sum_{n=2}^{5}(-3 x-4 n)$ $\newline$ Answer:

Full solution

More problems from Evaluate rational expressions II

Related topics

Evaluate:\newline∑n=25(−3x−4n) \sum_{n=2}^{5}(-3 x-4 n) n=2∑5​(−3x−4n)\newlineAnswer:

Evaluate: $\newline$ $\sum_{n=2}^{5}(-3 x-4 n)$ $\newline$ Answer: