AI tutor
Full solution
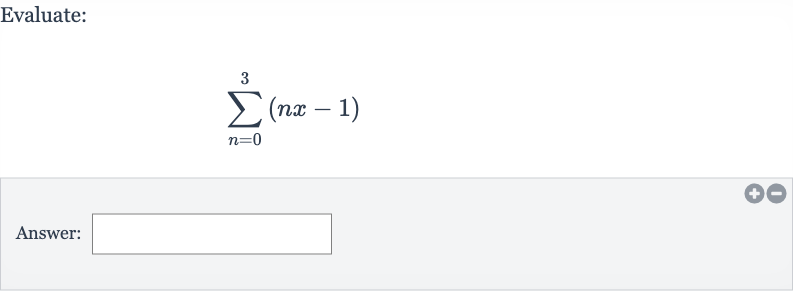
Q. Evaluate:Answer:
- Evaluate Term for : We need to evaluate the sum of the series given by the expression from to . We will do this by calculating the value of the expression for each value of and then summing those values.
- Calculate Term for : First, let's calculate the term for : .
- Compute Term for : Next, calculate the term for : .
- Determine Term for : Now, calculate the term for : .
- Sum Calculated Terms: Finally, calculate the term for : .
- Combine Like Terms: Now we sum all the terms we have calculated: .
- Combine Like Terms: Now we sum all the terms we have calculated: .Combine like terms: .