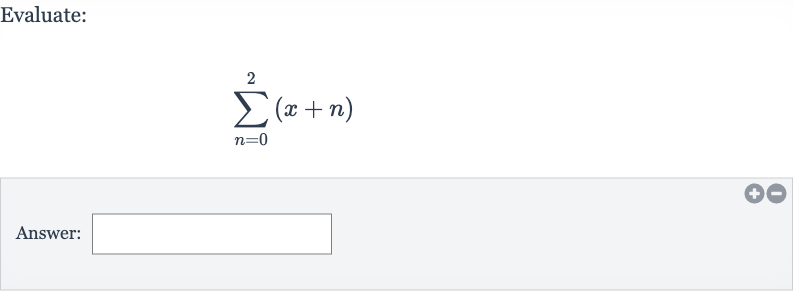AI tutor
Full solution
Q. Evaluate:Answer:
- Understand the problem: Understand the problem.We need to evaluate the sum of the expression as varies from to . This means we will substitute with , , and into the expression and add the results together.
- Substitute : Substitute into the expression.When , the expression becomes , which simplifies to .
- Substitute : Substitute into the expression.When , the expression becomes .
- Substitute : Substitute into the expression.When , the expression becomes .
- Add the results: Add the results from steps , , and .We add (from step ), (from step ), and (from step ) together: .
- Simplify the expression: Simplify the expression.Combining like terms, we get: .