AI tutor
Full solution
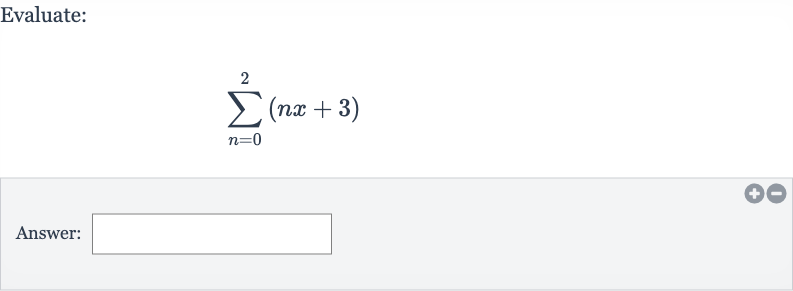
Q. Evaluate:Answer:
- Evaluate : Evaluate the expression for .When , the expression becomes , which simplifies to .
- Evaluate : Evaluate the expression for .When , the expression becomes , which simplifies to .
- Evaluate : Evaluate the expression for .When , the expression becomes , which simplifies to .
- Sum results to : Sum the results from to . Now we add the results from each step: . This simplifies to .
- Combine like terms: Combine like terms.Adding the constants: .Adding the terms: .So the sum is .
More problems from Evaluate rational expressions II
QuestionGet tutor help