AI tutor
Full solution
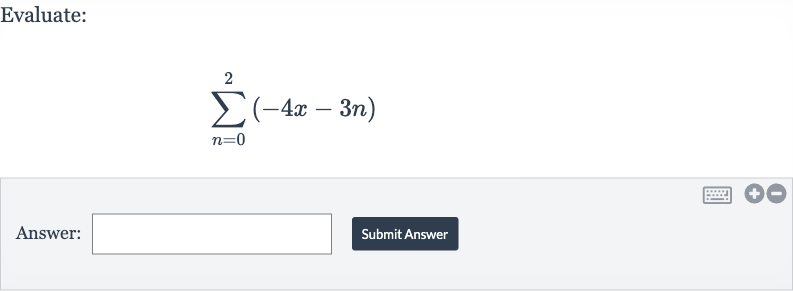
Q. Evaluate:Answer:Submit Answer
- Write Terms Explicitly: Write out the terms of the series explicitly.The series is , which means we need to evaluate for , , and , and then sum these values.
- Evaluate for : Evaluate the expression for , , and .For : For : For :
- Sum Evaluated Expressions: Sum the evaluated expressions.Sum = Sum =
- Combine Like Terms: Combine like terms.Sum =
- Check for Errors: Check for any mathematical errors in the previous steps. No errors were made in the calculations or the application of the summation.