AI tutor
Full solution
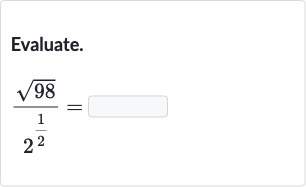
Q. Evaluate.
- Apply quotient rule of radical: Apply the quotient rule of radical to .
- Simplify denominator: Simplify the denominator.
- Find prime factorization of : Find the prime factorization of and try to make identical pairs of factors.= =
- Combine previous results: Combine the results from the previous steps.
- Simplify expression: Simplify the expression.