AI tutor
Full solution
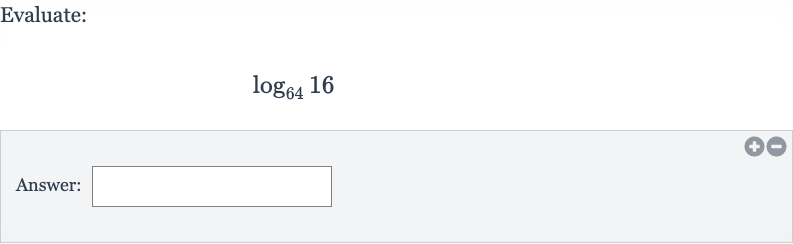
Q. Evaluate:Answer:
- Identify Relationship: Identify the relationship between the base of the logarithm and the number inside the logarithm.We have , which means we are looking for the power to which must be raised to get .We know that is raised to the th power () and is raised to the th power ().
- Express as Powers: Express both the base and the number inside the logarithm as powers of a common base. and . So, can be written as .
- Apply Change of Base: Apply the change of base formula for logarithms. The change of base formula states that can be written as , where is any positive number. Using as the new base, we get .
- Evaluate Using Common Base: Evaluate the logarithms using the common base . because . because .So, we have .
- Simplify Fraction: Simplify the fraction. simplifies to .Therefore, is equal to .