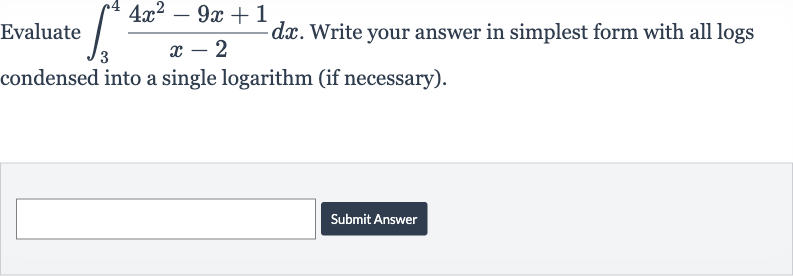
Evaluate int_(3)^(4)(4x^(2)-9x+1)/(x-2)dx. Write your answer in simplest form with all logs condensed into a single logarithm (if necessary). Submit Answer

Question

Evaluate  int_(3)^(4)(4x^(2)-9x+1)/(x-2)dx. Write your answer in simplest form with all logs condensed into a single logarithm (if necessary). Submit Answer

Bytelearn · Accepted Answer

Identify Integral: Identify the integral to be evaluated. We need to evaluate the integral of the function (4x^2 - 9x + 1)/(x - 2) from x = 3 to x = 4.Polynomial Long Division: Perform polynomial long division. Before integrating, we should simplify the integrand by performing polynomial long division of (4x^2 - 9x + 1) by (x - 2).Carry Out Division: Carry out the long division. Dividing 4x^2 by x gives 4x. Multiply (x - 2) by 4x to get 4x^2 - 8x. Subtract this from the original numerator to get -9x + 1 - (-8x) = -x + 1. Dividing -x by x gives -1. Multiply (x - 2) by -1 to get -x + 2. Subtract this from -x + 1 to get -1. So the quotient is 4x - 1 with a remainder of -1.Rewrite Integral: Rewrite the integral with the result of the division. The integral can now be written as the integral of 4x - 1 plus the integral of the remainder (-1) divided by (x - 2), from x = 3 to x = 4. ∫(4x - 1) dx + ∫(-1)/(x - 2) dx from x = 3 to x = 4.Integrate First Part: Integrate the first part of the expression. The integral of 4x - 1 with respect to x is 2x^2 - x. We will evaluate this from x = 3 to x = 4.Integrate Second Part: Integrate the second part of the expression. The integral of -1/(x - 2) with respect to x is -ln|x - 2|. We will evaluate this from x = 3 to x = 4.Evaluate Definite Integrals: Evaluate the definite integrals. First, evaluate 2x^2 - x from x = 3 to x = 4: (2(4)^2 - 4) - (2(3)^2 - 3) = (2*16 - 4) - (2*9 - 3) = (32 - 4) - (18 - 3) = 28 - 15 = 13. Next, evaluate -ln|x - 2| from x = 3 to x = 4: (-ln|4 - 2|) - (-ln|3 - 2|) = (-ln|2|) - (-ln|1|) = -ln(2) - (-ln(1)) = -ln(2) - 0 = -ln(2).Combine Results: Combine the results. The value of the integral is the sum of the results from steps 7 and 8: 13 - ln(2).

Evaluate $\int_{3}^{4} \frac{4 x^{2}-9 x+1}{x-2} d x$ . Write your answer in simplest form with all logs condensed into a single logarithm (if necessary). $\newline$ Submit Answer

Full solution

More problems from Evaluate rational expressions II

Related topics

Evaluate ∫344x2−9x+1x−2dx \int_{3}^{4} \frac{4 x^{2}-9 x+1}{x-2} d x ∫34​x−24x2−9x+1​dx. Write your answer in simplest form with all logs condensed into a single logarithm (if necessary).\newlineSubmit Answer

Evaluate $\int_{3}^{4} \frac{4 x^{2}-9 x+1}{x-2} d x$ . Write your answer in simplest form with all logs condensed into a single logarithm (if necessary). $\newline$ Submit Answer