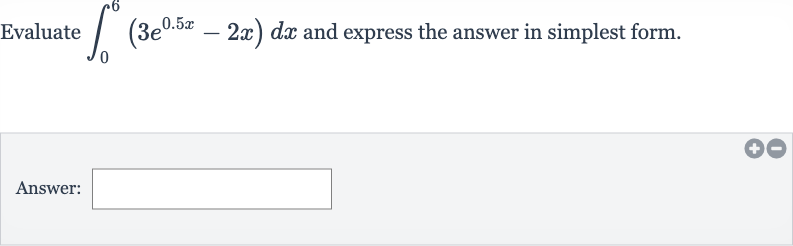
Evaluate int_(0)^(6)(3e^(0.5 x)-2x)dx and express the answer in simplest form. Answer:

Question

Evaluate  int_(0)^(6)(3e^(0.5 x)-2x)dx and express the answer in simplest form. Answer:

Bytelearn · Accepted Answer

Identify Integral: Identify the integral to be evaluated. We need to evaluate the integral of the function 3e^(0.5x) - 2x with respect to x from 0 to 6. The integral is written as ∫ from 0 to 6 of (3e^(0.5x) - 2x) dx.Break into Two: Break the integral into two separate integrals. We can separate the integral into two parts: one for 3e^(0.5x) and one for -2x. So, ∫ from 0 to 6 of (3e^(0.5x) - 2x) dx = ∫ from 0 to 6 of 3e^(0.5x) dx - ∫ from 0 to 6 of 2x dx.Evaluate First Integral: Evaluate the first integral ∫ from 0 to 6 of 3e^(0.5x) dx. To integrate 3e^(0.5x), we use the fact that the integral of e^(ax) is (1/a)e^(ax). Thus, the integral of 3e^(0.5x) is (3/(0.5))e^(0.5x) = 6e^(0.5x). Evaluating from 0 to 6 gives us 6e^(0.5*6) - 6e^(0.5*0).Evaluate Second Integral: Evaluate the second integral ∫ from 0 to 6 of 2x dx. The integral of 2x with respect to x is x^2. Evaluating from 0 to 6 gives us 6^2 - 0^2 = 36 - 0 = 36.Combine Results: Combine the results from Step 3 and Step 4. We have 6e^(0.5*6) - 6e^(0.5*0) - 36. Now we need to calculate the values of e^(0.5*6) and e^(0.5*0). e^(0.5*6) = e^3 and e^(0.5*0) = e^0 = 1. So, the result is 6e^3 - 6(1) - 36.Simplify Expression: Simplify the expression. 6e^3 - 6 - 36 = 6e^3 - 42. This is the final value of the definite integral.

Evaluate $\int_{0}^{6}\left(3 e^{0.5 x}-2 x\right) d x$ and express the answer in simplest form. $\newline$ Answer:

Full solution

More problems from Evaluate rational expressions II

Related topics

Evaluate ∫06(3e0.5x−2x)dx \int_{0}^{6}\left(3 e^{0.5 x}-2 x\right) d x ∫06​(3e0.5x−2x)dx and express the answer in simplest form.\newlineAnswer:

Evaluate $\int_{0}^{6}\left(3 e^{0.5 x}-2 x\right) d x$ and express the answer in simplest form. $\newline$ Answer: