AI tutor
Full solution
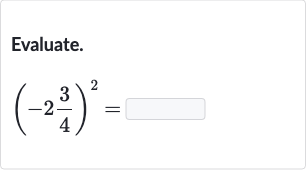
Q. Evaluate.
- Identify Base and Exponent: Identify the base and the exponent.In the expression , is the base raised to the exponent .Base: Exponent:
- Simplify Base: Simplify the base before applying the exponent.The base can be simplified by multiplying by .Simplified Base:
- Apply Exponent: Apply the exponent to the simplified base.Now we raise the simplified base to the power of . means is multiplied by itself.
- Multiply Fractions: Multiply the fractions.To multiply fractions, multiply the numerators together and the denominators together.
- Write Final Answer: Write the final answer.The simplest form of is .