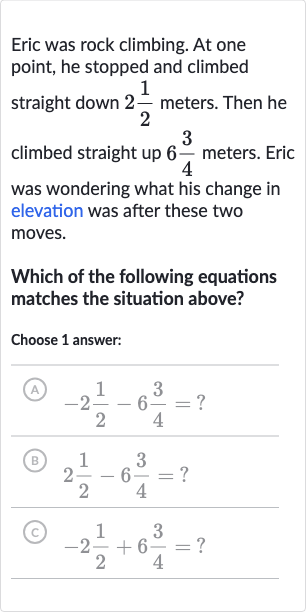
Eric was rock climbing. At one point, he stopped and climbed straight down 2(1)/(2) meters. Then he climbed straight up 6(3)/(4) meters. Eric was wondering what his change in elevation was after these two moves. Which of the following equations matches the situation above? Choose 1 answer: (A) -2(1)/(2)-6(3)/(4)= ? (B) 2(1)/(2)-6(3)/(4)= ? (c) -2(1)/(2)+6(3)/(4)= ?

Question

Eric was rock climbing. At one point, he stopped and climbed straight down  2(1)/(2) meters. Then he climbed straight up  6(3)/(4) meters. Eric was wondering what his change in elevation was after these two moves. Which of the following equations matches the situation above? Choose 1 answer: (A)  -2(1)/(2)-6(3)/(4)= ? (B)  2(1)/(2)-6(3)/(4)= ? (c)  -2(1)/(2)+6(3)/(4)= ?

Bytelearn · Accepted Answer

Climb Down: Eric first climbed down, which means his elevation decreased. Climbing down 2(1)/(2) meters can be represented as a negative change in elevation. Therefore, we write this as -2(1)/(2) meters.Climb Up: Next, Eric climbed up, which means his elevation increased. Climbing up 6(3)/(4) meters is a positive change in elevation. We represent this as +6(3)/(4) meters.Combine Changes: To find the total change in elevation, we need to combine these two changes. Since climbing down is a negative change and climbing up is a positive change, we add the two values together, taking into account their signs. The equation that matches the situation is -2(1)/(2) + 6(3)/(4) = ?.Convert to Fractions: Now we need to perform the calculation. First, we convert the mixed numbers to improper fractions to make the calculation easier.  2(1)/(2) = (2*2 + 1)/2 = 5/2  6(3)/(4) = (6*4 + 3)/4 = 27/4 The equation now looks like this: -5/2 + 27/4 = ?.Add Fractions: We need a common denominator to add these fractions. The common denominator for 2 and 4 is 4. We convert -5/2 to a fraction with a denominator of 4 by multiplying both the numerator and the denominator by 2. This gives us -10/4. The equation now looks like this: -10/4 + 27/4 = ?.Convert to Mixed Number: Now we can add the fractions since they have the same denominator.  -10/4 + 27/4 = (27 - 10)/4 = 17/4.Finally, we can convert the improper fraction back to a mixed number to find Eric's change in elevation.  17/4 = 4(1)/(4) or 4.25 meters. So, Eric's change in elevation is 4(1)/(4) meters.

Full solution

More problems from Solve a system of equations using any method: word problems

Related topics