Full solution
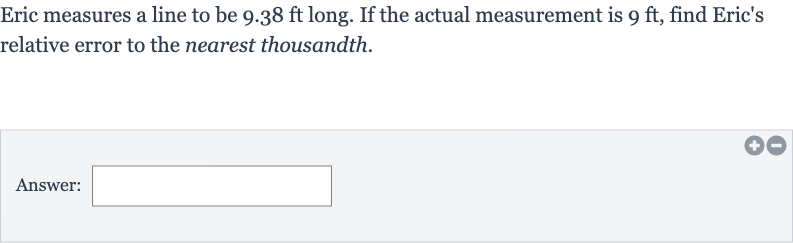
Q. Eric measures a line to be long. If the actual measurement is , find Eric's relative error to the nearest thousandth.Answer:
- Calculate Absolute Error: To find the relative error, we need to calculate the absolute error and then divide it by the true value. The absolute error is the difference between the measured value and the true value.Absolute error =
- Find Absolute Error: Now we calculate the absolute error using the values given.Absolute error =
- Calculate Relative Error: The absolute error is . Now we need to find the relative error by dividing the absolute error by the true value.Relative error = \frac{\text{Absolute error}}{\text{True Value}}
- Find Relative Error: We calculate the relative error using the absolute error we found and the true value.Relative error =
- Round Relative Error: Performing the division to find the relative error.
- Round Relative Error: Performing the division to find the relative error. Relative error = We need to round the relative error to the nearest thousandth as asked in the question prompt. Relative error (rounded) =
More problems from Interpret confidence intervals for population means
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help