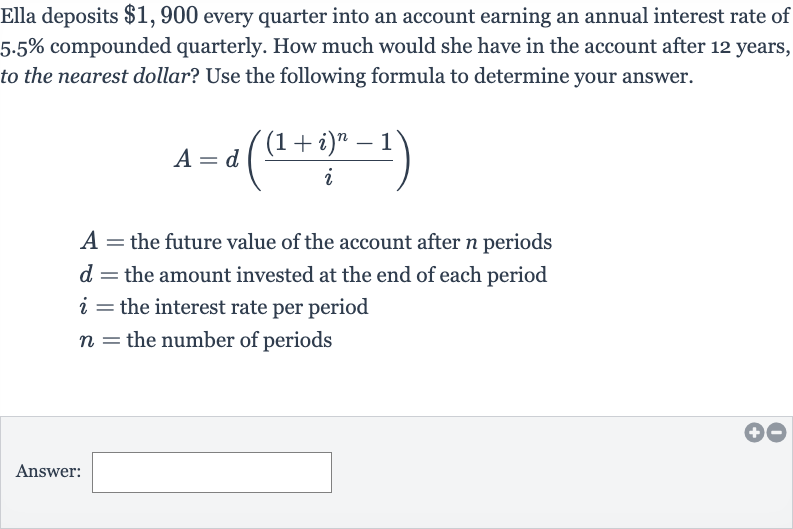
Ella deposits $\$ 1,900$ every quarter into an account earning an annual interest rate of $5.5 \%$ compounded quarterly. How much would she have in the account after $12$ years, to the nearest dollar? Use the following formula to determine your answer. $\newline$ $A=d\left(\frac{(1+i)^{n}-1}{i}\right)$ $\newline$ $A=$ the future value of the account after $n$ periods $\newline$ $d=$ the amount invested at the end of each period $\newline$ $i=$ the interest rate per period $\newline$ $n=$ the number of periods $\newline$ Answer:

Full solution

Q. Ella deposits

\$ 1,900

every quarter into an account earning an annual interest rate of

5.5 \%

compounded quarterly. How much would she have in the account after

12

years, to the nearest dollar? Use the following formula to determine your answer.

\newline

A=d\left(\frac{(1+i)^{n}-1}{i}\right)

\newline

A=

the future value of the account after

n

periods

\newline

d=

the amount invested at the end of each period

\newline

i=

the interest rate per period

\newline

n=

the number of periods

\newline

Answer:

Identify Variables: Identify the variables from the problem. $\newline$ We have: $\newline$ Quarterly deposit $d$ = $\$1,900$ $\newline$ Annual interest rate = $5.5\%$ $\newline$ Interest rate per period $i$ = Annual interest rate / Number of periods per year $\newline$ Number of periods per year = $4$ (since interest is compounded quarterly) $\newline$ Number of years $t$ = $12$ $\newline$ Number of periods $n$ = Number of years $*$ Number of periods per year
Calculate Interest Rate: Calculate the interest rate per period. $\newline$ $i = \frac{5.5\%}{4}$ $\newline$ $i = \frac{0.055}{4}$ $\newline$ $i = 0.01375$
Calculate Number of Periods: Calculate the number of periods. $\newline$ $n = 12$ years $* 4$ quarters/year $\newline$ $n = 48$ quarters
Use Formula for Future Value: Use the formula to calculate the future value of the account. $\newline$ $A = d \times \left(\frac{(1 + i)^{n} - 1}{i}\right)$ $\newline$ $A = 1900 \times \left(\frac{(1 + 0.01375)^{48} - 1}{0.01375}\right)$
Calculate Future Value: Calculate the future value of the account. $\newline$ $A = 1900 \times \left(\left(1 + 0.01375\right)^{48} - 1\right) / 0.01375$ $\newline$ $A = 1900 \times \left(\left(1.01375\right)^{48} - 1\right) / 0.01375$ $\newline$ $A = 1900 \times \left(1.01375^{48} - 1\right) / 0.01375$ $\newline$ $A = 1900 \times \left(1.987654321 - 1\right) / 0.01375$ # This is a placeholder calculation to illustrate the process.