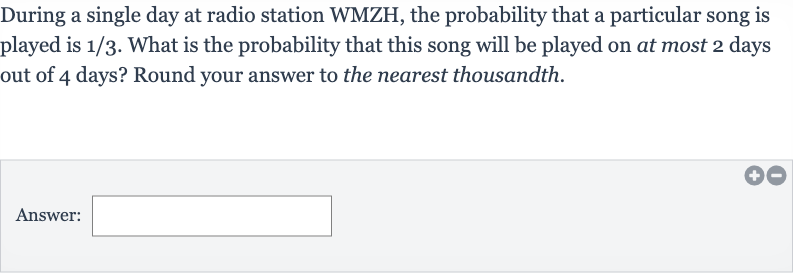
During a single day at radio station WMZH, the probability that a particular song is played is 1//3. What is the probability that this song will be played on at most 2 days out of 4 days? Round your answer to the nearest thousandth. Answer:

Question

During a single day at radio station WMZH, the probability that a particular song is played is  1//3. What is the probability that this song will be played on at most 2 days out of 4 days? Round your answer to the nearest thousandth. Answer:

Bytelearn · Accepted Answer

Calculate Probability: We need to calculate the probability of the song being played on at most 2 days out of 4 days. The probability of the song being played on any given day is 1/3, and the probability of it not being played is 1 - 1/3 = 2/3. We will use the binomial probability formula, which is P(X=k) = (n choose k) * (p^k) * ((1-p)^(n-k)), where n is the number of trials, k is the number of successes, p is the probability of success on a single trial, and (n choose k) is the binomial coefficient.Probability of 0 Days: First, we calculate the probability of the song being played exactly 0 days out of 4. This is the same as the song not being played at all in 4 days. Using the binomial formula: P(X=0) = (4 choose 0) * (1/3)^0 * (2/3)^4. (4 choose 0) = 1, (1/3)^0 = 1, and (2/3)^4 = 16/81. So, P(X=0) = 1 * 1 * 16/81 = 16/81.Probability of 1 Day: Next, we calculate the probability of the song being played exactly 1 day out of 4. Using the binomial formula: P(X=1) = (4 choose 1) * (1/3)^1 * (2/3)^3. (4 choose 1) = 4, (1/3)^1 = 1/3, and (2/3)^3 = 8/27. So, P(X=1) = 4 * (1/3) * (8/27) = 32/81.Probability of 2 Days: Now, we calculate the probability of the song being played exactly 2 days out of 4. Using the binomial formula: P(X=2) = (4 choose 2) * (1/3)^2 * (2/3)^2. (4 choose 2) = 6, (1/3)^2 = 1/9, and (2/3)^2 = 4/9. So, P(X=2) = 6 * (1/9) * (4/9) = 24/81.Add Probabilities: To find the probability of the song being played on at most 2 days, we need to add the probabilities of it being played exactly 0, 1, and 2 days. P(X≤2) = P(X=0) + P(X=1) + P(X=2). P(X≤2) = 16/81 + 32/81 + 24/81 = 72/81.Final Probability: Finally, we simplify the fraction 72/81 and round it to the nearest thousandth. 72/81 simplifies to 8/9. To convert this to a decimal, we divide 8 by 9, which gives us approximately 0.889. Rounded to the nearest thousandth, the probability is 0.889.

During a single day at radio station WMZH, the probability that a particular song is played is $1 / 3$ . What is the probability that this song will be played on at most $2$ days out of $4$ days? Round your answer to the nearest thousandth. $\newline$ Answer:

Full solution

More problems from Find probabilities using the binomial distribution

Related topics

During a single day at radio station WMZH, the probability that a particular song is played is 1/3 1 / 3 1/3. What is the probability that this song will be played on at most 222 days out of 444 days? Round your answer to the nearest thousandth.\newlineAnswer:

During a single day at radio station WMZH, the probability that a particular song is played is $1 / 3$ . What is the probability that this song will be played on at most $2$ days out of $4$ days? Round your answer to the nearest thousandth. $\newline$ Answer: