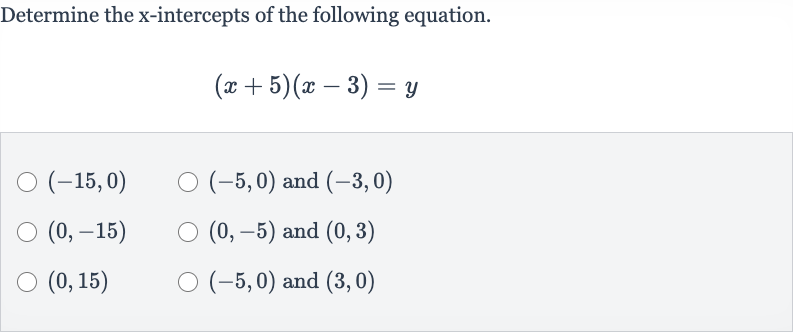Full solution
Q. Determine the -intercepts of the following equation. and and and
- Set to : To find the -intercepts of the equation, we need to set to and solve for .
- Apply Zero Product Property: Now we have a product of two factors equal to zero. According to the zero product property, if the product of two factors is zero, then at least one of the factors must be zero.So, we set each factor equal to zero and solve for . or
- Solve for x: Solving the first equation for x gives us the first x-intercept:
- First x-intercept: Solving the second equation for x gives us the second x-intercept:
- Second x-intercept: We have found the two x-intercepts of the equation . They are and . Therefore, the x-intercepts are the points and .
More problems from Write a quadratic function from its x-intercepts and another point
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help