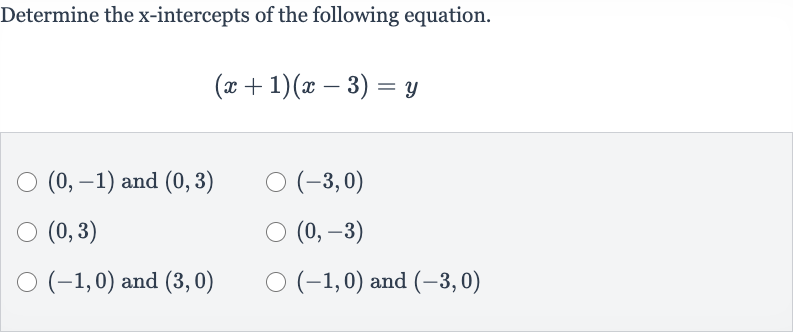Full solution
Q. Determine the -intercepts of the following equation. and and and
- Identify x-intercepts: Identify the x-intercepts. The x-intercepts occur where the graph of the equation crosses the x-axis, which is where . So, we set to and solve for in the equation .
- Solve for x: Solve the equation for x.We have .To find the x-intercepts, we set each factor equal to zero and solve for x. or
- Find first x-intercept: Find the first x-intercept.Solving gives us .So, one x-intercept is .
- Find second x-intercept: Find the second x-intercept.Solving gives us .So, the second x-intercept is .
More problems from Write a quadratic function from its x-intercepts and another point
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help