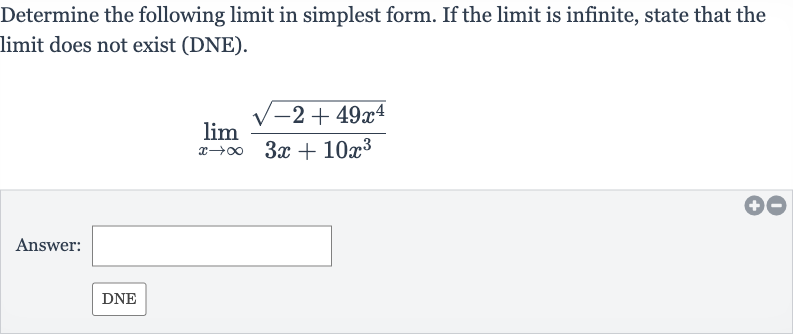
Determine the following limit in simplest form. If the limit is infinite, state that the limit does not exist (DNE). lim_(x rarr oo)(sqrt(-2+49x^(4)))/(3x+10x^(3)) Answer:

Question

Determine the following limit in simplest form. If the limit is infinite, state that the limit does not exist (DNE).  lim_(x rarr oo)(sqrt(-2+49x^(4)))/(3x+10x^(3)) Answer:

Bytelearn · Accepted Answer

Identify highest power: We are asked to find the limit of the function (sqrt(-2+49x^(4)))/(3x+10x^(3)) as x approaches infinity. To do this, we will first identify the highest power of x in both the numerator and the denominator.Divide by x^3: The highest power of x in the numerator inside the square root is x^4, and in the denominator, it is x^3. To simplify the limit, we will divide both the numerator and the denominator by x^3, the highest power in the denominator.Simplify expression: Dividing each term by x^3 gives us the following expression: lim_(x rarr oo)(sqrt((-2/x^3)+49x))/(3+(10x^2))Take square root: As x approaches infinity, the term (-2/x^3) approaches 0, so we can simplify the expression to: lim_(x rarr oo)(sqrt(49x))/(3+(10x^2))Divide by x^(1/2): We can take the square root of 49x, which is 7x^(1/2), and rewrite the expression as: lim_(x rarr oo)(7x^(1/2))/(3+(10x^2))Approach infinity: Now, we divide the numerator and the denominator by x^(1/2), the highest power of x in the numerator: lim_(x rarr oo)(7)/(3/x^(1/2)+10x^(3/2))Limit is 0: As x approaches infinity, the term (3/x^(1/2)) approaches 0, and we are left with: lim_(x rarr oo)(7)/(10x^(3/2))Now, as x approaches infinity, the denominator (10x^(3/2)) grows without bound, and the entire expression approaches 0. Therefore, the limit is 0.

Determine the following limit in simplest form. If the limit is infinite, state that the limit does not exist (DNE). $\newline$ $\lim _{x \rightarrow \infty} \frac{\sqrt{-2+49 x^{4}}}{3 x+10 x^{3}}$ $\newline$ Answer:

Full solution

More problems from Power rule

Related topics

Determine the following limit in simplest form. If the limit is infinite, state that the limit does not exist (DNE).\newlinelim⁡x→∞−2+49x43x+10x3 \lim _{x \rightarrow \infty} \frac{\sqrt{-2+49 x^{4}}}{3 x+10 x^{3}} x→∞lim​3x+10x3−2+49x4​​\newlineAnswer:

Determine the following limit in simplest form. If the limit is infinite, state that the limit does not exist (DNE). $\newline$ $\lim _{x \rightarrow \infty} \frac{\sqrt{-2+49 x^{4}}}{3 x+10 x^{3}}$ $\newline$ Answer: