Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

d(n)=(5)/(16)(2)^(n-1) What is the 5^("th ") term in the sequence?

d(n)=516(2)n−1 d(n)=\frac{5}{16}(2)^{n-1} \newlineWhat is the 5th  5^{\text {th }} term in the sequence?

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 1right chevron icon
Geometric sequencesright chevron icon

Full solution

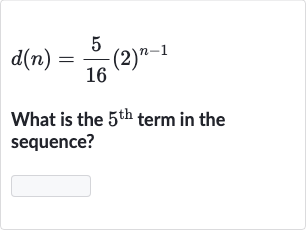
Q. d(n)=516(2)n−1 d(n)=\frac{5}{16}(2)^{n-1} \newlineWhat is the 5th  5^{\text {th }} term in the sequence?
  1. Substitute n=5n=5: To find the 5th5^{\text{th}} term in the sequence, we need to substitute n=5n=5 into the formula d(n)=516(2)n−1d(n)=\frac{5}{16}(2)^{n-1}.
  2. Calculate the exponent: Substitute n=5n=5 into the formula: d(5)=516(2)5−1d(5)=\frac{5}{16}(2)^{5-1}.
  3. Calculate 242^4: Calculate the exponent: 2(5−1)=242^{(5-1)} = 2^4.
  4. Multiply the result: Calculate 242^4: 24=2×2×2×2=162^4 = 2 \times 2 \times 2 \times 2 = 16.
  5. Simplify the expression: Multiply the result by (5)/(16)(5)/(16): d(5)=(5)/(16)×16d(5) = (5)/(16) \times 16.
  6. Expression simplifies to: Simplify the expression: (516)×16=5×(1616)(\frac{5}{16}) \times 16 = 5 \times (\frac{16}{16}).
  7. Final result: Since (16)/(16)(16)/(16) equals 11, the expression simplifies to: 5×1=55 \times 1 = 5.

More problems from Geometric sequences

Question
Find the sum of the finite arithmetic series. ∑n=110(7n+4)\sum_{n=1}^{10} (7n+4)\newline______
Get tutor helpright-arrow

Posted 6 months ago

Question
Type the missing number in this sequence: `55,\59,\63,\text{_____},\71,\75,\79`
Get tutor helpright-arrow

Posted 2 months ago

Question
Type the missing number in this sequence: `2, 4 8`, ______,`32`
Get tutor helpright-arrow

Posted 2 months ago

Question
What kind of sequence is this? 2,10,50,250,…2, 10, 50, 250, \ldots Choices:Choices:\newline[A]arithmetic\text{[A]arithmetic}\newline[B]geometric\text{[B]geometric}\newline[C]both\text{[C]both}\newline[D]neither\text{[D]neither}
Get tutor helpright-arrow

Posted 2 months ago

Question
What is the missing number in this pattern? 1,4,9,16,25,36,49,64,81,____1, 4, 9, 16, 25, 36, 49, 64, 81, \_\_\_\_
Get tutor helpright-arrow

Posted 5 months ago

Question
Classify the series. ∑n=012(n+2)3 \sum_{n = 0}^{12} (n + 2)^3 \newlineChoices:\newline[A]arithmetic\text{[A]arithmetic}\newline[B]geometric\text{[B]geometric}\newline[C]both\text{[C]both}\newline[D]neither\text{[D]neither}
Get tutor helpright-arrow

Posted 2 months ago

Question
Find the first three partial sums of the series.\newline1+6+11+16+21+26+⋯1 + 6 + 11 + 16 + 21 + 26 + \cdots\newlineWrite your answers as integers or fractions in simplest form.\newlineS1=S_1 = ____\newlineS2=S_2 = ____\newlineS3=S_3 = ____
Get tutor helpright-arrow

Posted 5 months ago

Question
Find the third partial sum of the series. \newline3+9+15+21+27+33+⋯3 + 9 + 15 + 21 + 27 + 33 + \cdots\newlineWrite your answer as an integer or a fraction in simplest form. \newlineS3=S_3 = ____
Get tutor helpright-arrow

Posted 5 months ago

Question
Find the first three partial sums of the series. \newline1+7+13+19+25+31+⋯1 + 7 + 13 + 19 + 25 + 31 + \cdots\newlineWrite your answers as integers or fractions in simplest form. \newlineS1=S_1 = ____\newlineS2=S_2 = ____\newlineS3=S_3 = ____
Get tutor helpright-arrow

Posted 6 months ago

Question
Does the infinite geometric series converge or diverge?\newline1+34+916+2764+⋯1 + \frac{3}{4} + \frac{9}{16} + \frac{27}{64} + \cdots\newlineChoices:\newline[A]converge\text{[A]converge}\newline[B]diverge\text{[B]diverge}
Get tutor helpright-arrow

Posted 2 months ago

View all (131)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant