Full solution
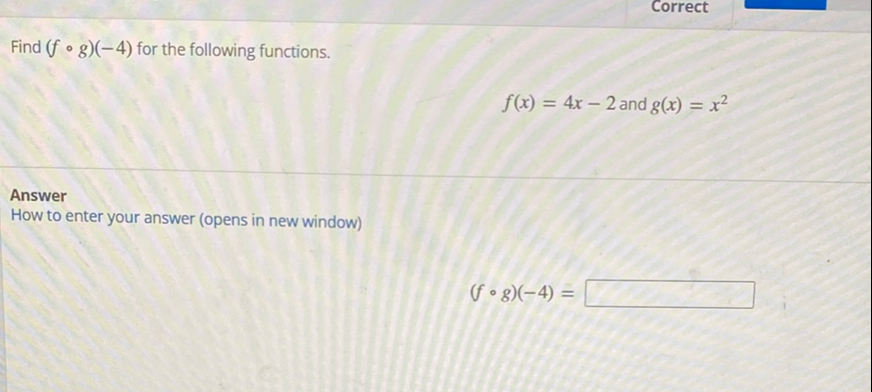
Q. Find for the following functions.AnswerHow to enter your answer (opens in new window)
- Understand Function Composition: First, we need to understand what means. The notation represents the composition of the functions and , which means we first apply to , and then apply to the result of . So, . Let's start by finding .
- Calculate : Calculate by substituting with in the function ..
- Find : Now that we have , we can find by applying to the result of . So we need to substitute with in the function ..
- Calculate : Calculate by multiplying with and then subtracting ..
More problems from Find trigonometric ratios using reference angles
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
Question
. Find the value of in degrees.Write your answer in simplified, rationalized form. Do not round.____
Get tutor helpQuestionGet tutor help