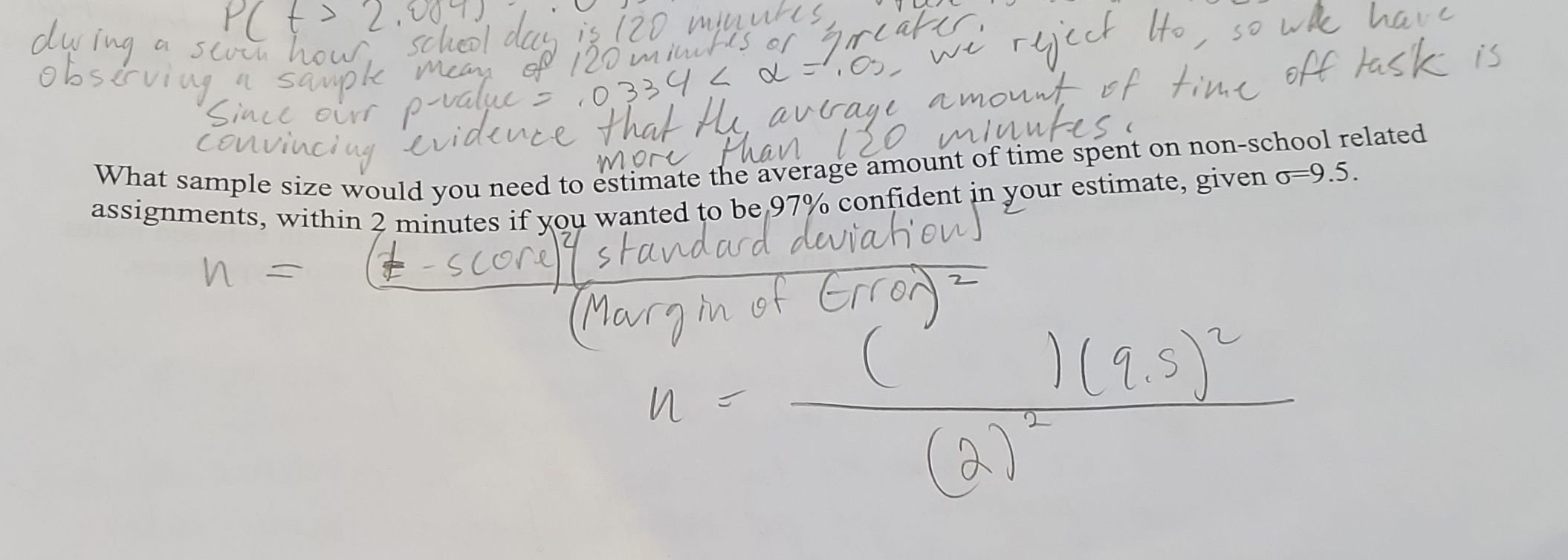What sample size would you need to estimate the average amount of time spent on non-school related assignments, within 2 minutes if you wanted to be 97% confident in your estimate, given sigma=9.5.

Question

Bytelearn · Accepted Answer

Identify Formula: Identify the formula to calculate the sample size for estimating a population mean with a certain level of confidence. The formula is: n = (Z * σ / E)^2 where n is the sample size, Z is the z-score corresponding to the desired confidence level, σ is the population standard deviation, and E is the margin of error (the maximum allowable error in the estimate).Determine Z-Score: Determine the z-score corresponding to a 97% confidence level. This can be found using a z-table or a statistical calculator. For a 97% confidence level, the z-score is approximately 2.17.Plug Known Values: Plug the known values into the formula. We have σ = 9.5 (the standard deviation) and E = 2 (the desired margin of error). Now we can substitute these values into the formula: n = (2.17 * 9.5 / 2)^2Perform Calculations: Perform the calculations step by step. First, calculate the numerator of the fraction: 2.17 * 9.5 = 20.615 Next, divide by the margin of error, E: 20.615 / 2 = 10.3075 Finally, square the result to find n: 10.3075^2 = 106.2445625Round Sample Size: Since the sample size must be a whole number, and you cannot have a fraction of a sample, round up to the nearest whole number. This ensures that the sample size is not smaller than needed for the desired confidence level. n = 107 (rounded up from 106.2445625)

What sample size would you need to estimate the average amount of time spent on non-school related assignments, within $2$ minutes if you wanted to be $97 \%$ confident in your estimate, given $\sigma=9.5$ .

Full solution

More problems from Percent error: word problems

Related topics

What sample size would you need to estimate the average amount of time spent on non-school related assignments, within 222 minutes if you wanted to be 97% 97 \% 97% confident in your estimate, given σ=9.5 \sigma=9.5 σ=9.5.

What sample size would you need to estimate the average amount of time spent on non-school related assignments, within $2$ minutes if you wanted to be $97 \%$ confident in your estimate, given $\sigma=9.5$ .