Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

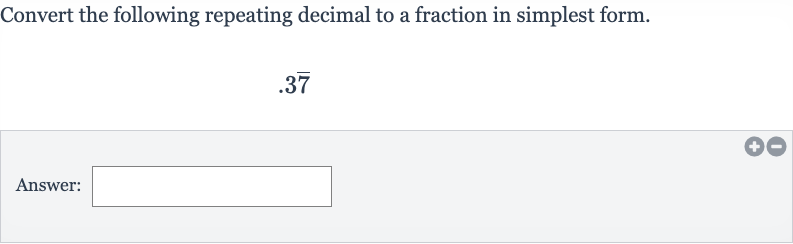
Convert the following repeating decimal to a fraction in simplest form. .3 bar(7) Answer:

Convert the following repeating decimal to a fraction in simplest form.\newline.37‾ .3 \overline{7} \newlineAnswer:

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Precalculusright chevron icon
Partial sums of geometric seriesright chevron icon

Full solution

Q. Convert the following repeating decimal to a fraction in simplest form.\newline.37‾ .3 \overline{7} \newlineAnswer:
  1. Assign xx as decimal: Let xx equal the repeating decimal 0.370.37 with the 77 repeating indefinitely, so x=0.3777…x = 0.3777\ldots
  2. Multiply xx by 1010: To isolate the repeating part, we multiply xx by 1010, since there is one digit in the repeating cycle. This gives us 10x=3.7777…10x = 3.7777\ldots
  3. Subtract xx from 10x10x: Now we subtract the original xx from 10x10x to get rid of the repeating part: 10x−x=3.7777...−0.3777...10x - x = 3.7777... - 0.3777...
  4. Solve for x: Performing the subtraction, we get 9x=3.49x = 3.4 because the infinite repeating 77s cancel each other out.
  5. Express as fraction: Now we solve for xx by dividing both sides of the equation by 99: x=3.49x = \frac{3.4}{9}
  6. Simplify fraction: To express 3.43.4 as a fraction, we write it as 3410\frac{34}{10} because moving the decimal point two places to the right converts it to an integer.
  7. Find GCD: Now we have x=3410/9x = \frac{34}{10} / 9. To simplify this, we multiply the numerator by the reciprocal of the denominator: x=3410×19x = \frac{34}{10} \times \frac{1}{9}
  8. Divide by GCD: Multiplying the fractions, we get x=34(10×9)=3490x = \frac{34}{(10 \times 9)} = \frac{34}{90}
  9. Divide by GCD: Multiplying the fractions, we get x=34(10×9)=3490x = \frac{34}{(10 \times 9)} = \frac{34}{90} We simplify the fraction 3490\frac{34}{90} by finding the greatest common divisor (GCD) of 3434 and 9090, which is 22.
  10. Divide by GCD: Multiplying the fractions, we get x=34(10×9)=3490x = \frac{34}{(10 \times 9)} = \frac{34}{90} We simplify the fraction 3490\frac{34}{90} by finding the greatest common divisor (GCD) of 3434 and 9090, which is 22. Dividing both the numerator and the denominator by the GCD, we get x=(34/2)(90/2)=1745x = \frac{(34/2)}{(90/2)} = \frac{17}{45}

More problems from Partial sums of geometric series

Question
Find the sum of the finite arithmetic series. ∑n=110(7n+4)\sum_{n=1}^{10} (7n+4)\newline______
Get tutor helpright-arrow

Posted 9 months ago

Question
Type the missing number in this sequence: `55,\59,\63,\text{_____},\71,\75,\79`
Get tutor helpright-arrow

Posted 5 months ago

Question
Type the missing number in this sequence: `2, 4 8`, ______,`32`
Get tutor helpright-arrow

Posted 5 months ago

Question
What kind of sequence is this? 2,10,50,250,…2, 10, 50, 250, \ldots Choices:Choices:\newline[A]arithmetic\text{[A]arithmetic}\newline[B]geometric\text{[B]geometric}\newline[C]both\text{[C]both}\newline[D]neither\text{[D]neither}
Get tutor helpright-arrow

Posted 5 months ago

Question
What is the missing number in this pattern? 1,4,9,16,25,36,49,64,81,____1, 4, 9, 16, 25, 36, 49, 64, 81, \_\_\_\_
Get tutor helpright-arrow

Posted 7 months ago

Question
Classify the series. ∑n=012(n+2)3 \sum_{n = 0}^{12} (n + 2)^3 \newlineChoices:\newline[A]arithmetic\text{[A]arithmetic}\newline[B]geometric\text{[B]geometric}\newline[C]both\text{[C]both}\newline[D]neither\text{[D]neither}
Get tutor helpright-arrow

Posted 5 months ago

Question
Find the first three partial sums of the series.\newline1+6+11+16+21+26+⋯1 + 6 + 11 + 16 + 21 + 26 + \cdots\newlineWrite your answers as integers or fractions in simplest form.\newlineS1=S_1 = ____\newlineS2=S_2 = ____\newlineS3=S_3 = ____
Get tutor helpright-arrow

Posted 7 months ago

Question
Find the third partial sum of the series. \newline3+9+15+21+27+33+⋯3 + 9 + 15 + 21 + 27 + 33 + \cdots\newlineWrite your answer as an integer or a fraction in simplest form. \newlineS3=S_3 = ____
Get tutor helpright-arrow

Posted 7 months ago

Question
Find the first three partial sums of the series. \newline1+7+13+19+25+31+⋯1 + 7 + 13 + 19 + 25 + 31 + \cdots\newlineWrite your answers as integers or fractions in simplest form. \newlineS1=S_1 = ____\newlineS2=S_2 = ____\newlineS3=S_3 = ____
Get tutor helpright-arrow

Posted 9 months ago

Question
Does the infinite geometric series converge or diverge?\newline1+34+916+2764+⋯1 + \frac{3}{4} + \frac{9}{16} + \frac{27}{64} + \cdots\newlineChoices:\newline[A]converge\text{[A]converge}\newline[B]diverge\text{[B]diverge}
Get tutor helpright-arrow

Posted 5 months ago

View all (96)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant