Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

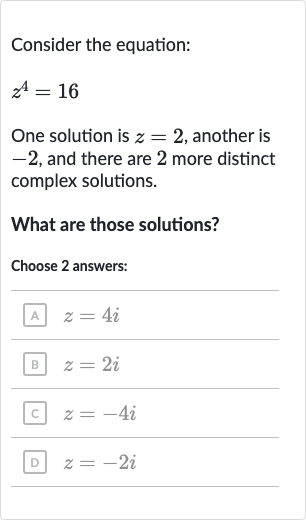
Consider the equation:

z^(4)=16
One solution is
z=2, another is -2 , and there are 2 more distinct complex solutions.
What are those solutions?
Choose 2 answers:
A
z=4i
B
z=2i
c.
z=-4i
D
z=-2i

Consider the equation: $\newline$ $z^{4}=16$ $\newline$ One solution is $z=2$ , another is $-2$ , and there are $2$ more distinct complex solutions. $\newline$ What are those solutions? $\newline$ Choose $\mathbf{2}$ answers: $\newline$ A $z=4 i$ $\newline$ B $z=2 i$ $\newline$ c. $z=-4 i$ $\newline$ D $z=-2 i$

View step-by-step help

View step-by-step help

Solve rational equations

Full solution

Q. Consider the equation:

\newline

z^{4}=16

\newline

One solution is

z=2

, another is

-2

, and there are

2

more distinct complex solutions.

\newline

What are those solutions?

\newline

Choose

\mathbf{2}

answers:

\newline

A

z=4 i

\newline

B

z=2 i

\newline

c.

z=-4 i

\newline

D

z=-2 i

Identify type of solutions: Write down the given equation and identify the type of solutions we are looking for. $\newline$ The given equation is $z^{4} = 16$ . We know that $z = 2$ and $z = -2$ are real solutions to this equation. Since the equation is a polynomial of degree $4$ , it must have $4$ solutions in total (counting multiplicity) according to the Fundamental Theorem of Algebra. We are looking for the two complex solutions that are not real.
Express equation in complex form: Express the equation in its complex form. $\newline$ The equation $z^{4} = 16$ can be rewritten as $z^{4} - 16 = 0$ . This is a difference of squares and can be factored as $(z^2 - 4)(z^2 + 4) = 0$ .
Solve for $z$ when $z^2 - 4 = 0$ : Solve for $z$ when $z^2 - 4 = 0$ . We already know the solutions for $z^2 - 4 = 0$ are $z = 2$ and $z = -2$ . These are the real solutions.
Solve for $z$ when $z^2 + 4 = 0$ : Solve for $z$ when $z^2 + 4 = 0$ . To find the complex solutions, we solve the equation $z^2 + 4 = 0$ . This gives us $z^2 = -4$ . Taking the square root of both sides, we get $z = \pm\sqrt{-4}$ .
Calculate square root of $-4$ : Calculate the square root of $-4$ . The square root of $-4$ is $2i$ , where $i$ is the imaginary unit. Therefore, the two complex solutions are $z = 2i$ and $z = -2i$ .
Match solutions with options: Match the solutions with the given options. $\newline$ The solutions we found are $z = 2i$ and $z = -2i$ . These correspond to options $B$ and $D$ .

More problems from Solve rational equations

Question

Evaluate the expression for

t = -4.4

\newline

Write your answer in simplest form.

\newline

` frac{t - 4}{t - 2} =` ____

Posted 1 month ago

Question

Simplify. Write your answer using whole numbers and variables.

\newline

\frac{g}{3g^2 - 4g}

Posted 2 months ago

Question

Simplify. Express your answer as a single fraction in simplest form.

\frac{3}{2} - \frac{5p^3}{3}

Posted 2 months ago

Question

Simplify. Express your answer as a single fraction in simplest form.

\newline

\frac{1 + \frac{v^5w}{3}}{1}

\newline

Posted 2 months ago

Question

h

\newline

\frac{-5}{h - 2} = \frac{-4}{h - 3}

\newline

1

2

\newline

h =

h =

Posted 1 month ago

Question

What is the equation of the vertical asymptote of

y = \frac{1}{x + 9}

Posted 2 months ago

Question

What is the excluded value for

y = \frac{1}{x - 9} - 9

\newline

Posted 2 months ago

Question

Simplify. Write your answer using whole numbers and variables.

\newline

\frac{9k + 4}{9k^2 + 4k}

\newline

Posted 2 months ago

Question

Divide. Write your answer in simplest form.

\newline

\frac{g- 1}{10g^3 + 25g^2} \div (g- 1)

\newline

Posted 2 months ago

Question

Simplify. Express your answer as a single fraction in simplest form.

\newline

\frac{5 - \frac{3}{t^3}}{1}

\newline

Posted 2 months ago