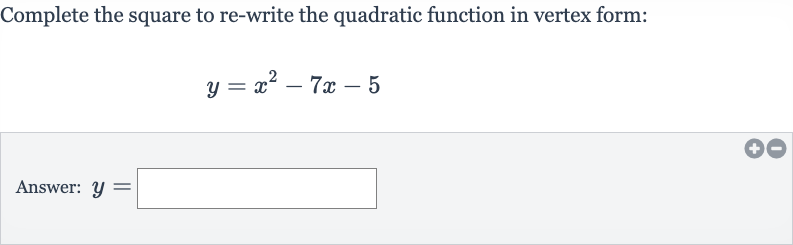
Complete the square to re-write the quadratic function in vertex form: y=x^(2)-7x-5 Answer: y=

Question

Complete the square to re-write the quadratic function in vertex form:  y=x^(2)-7x-5 Answer:  y=

Bytelearn · Accepted Answer

Form Perfect Square Trinomial: To complete the square, we need to form a perfect square trinomial from the quadratic and linear terms of the function y = x^2 - 7x - 5. We will add and subtract the square of half the coefficient of x inside the parentheses.Calculate and Add/Subtract: First, we take the coefficient of x, which is -7, divide it by 2 to get -7/2, and then square it to get (-7/2)^2 = 49/4. We will add and subtract this value inside the equation.Rewrite Function with Added Terms: We rewrite the function by adding and subtracting 49/4 inside the equation: y = x^2 - 7x + 49/4 - 49/4 - 5Group and Combine Constants: Now, we group the perfect square trinomial and combine the constants: y = (x^2 - 7x + 49/4) - 49/4 - 5Factor Perfect Square Trinomial: Next, we factor the perfect square trinomial: y = (x - 7/2)^2 - 49/4 - 5Convert Constant to Common Denominator: To combine the constants, we need a common denominator. The common denominator for 4 and 1 (since 5 can be written as 5/1) is 4. So we convert -5 to -20/4: y = (x - 7/2)^2 - 49/4 - 20/4Combine Constants: Now, we combine the constants -49/4 and -20/4: y = (x - 7/2)^2 - 69/4Write in Vertex Form: The quadratic function is now written in vertex form, which is y = a(x - h)^2 + k, where (h, k) is the vertex of the parabola. In this case, a = 1, h = 7/2, and k = -69/4.

Complete the square to re-write the quadratic function in vertex form: $\newline$ $y=x^{2}-7 x-5$ $\newline$ Answer: $y=$

Full solution

More problems from Csc, sec, and cot of special angles

Related topics

Complete the square to re-write the quadratic function in vertex form:\newliney=x2−7x−5 y=x^{2}-7 x-5 y=x2−7x−5\newlineAnswer: y= y= y=

Complete the square to re-write the quadratic function in vertex form: $\newline$ $y=x^{2}-7 x-5$ $\newline$ Answer: $y=$