Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

c(n)=(4)/(9)(-3)^(n-1) What is the 3^("rd ") term in the sequence?

c(n)=49(−3)n−1 c(n)=\frac{4}{9}(-3)^{n-1} \newlineWhat is the 3rd  3^{\text {rd }} term in the sequence?

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 1right chevron icon
Geometric sequencesright chevron icon

Full solution

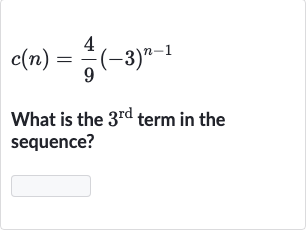
Q. c(n)=49(−3)n−1 c(n)=\frac{4}{9}(-3)^{n-1} \newlineWhat is the 3rd  3^{\text {rd }} term in the sequence?
  1. Identify term of sequence: Identify the term of the sequence we need to find.\newlineWe are asked to find the 3rd3^{\text{rd}} term in the sequence defined by the formula c(n)=(49)(−3)n−1c(n) = \left(\frac{4}{9}\right)(-3)^{n-1}.
  2. Substitute term number: Substitute the term number into the formula.\newlineTo find the 3rd3^{\text{rd}} term, we substitute n=3n=3 into the formula c(n)=(49)(−3)(n−1)c(n)=\left(\frac{4}{9}\right)(-3)^{(n-1)}.\newlinec(3)=(49)(−3)(3−1)c(3)=\left(\frac{4}{9}\right)(-3)^{(3-1)}
  3. Calculate the exponent: Calculate the exponent.\newlineCalculate the value of (−3)(3−1)(-3)^{(3-1)}, which is (−3)2(-3)^2.\newline(−3)2=9(-3)^2 = 9
  4. Multiply by coefficient: Multiply the result of the exponentiation by the coefficient.\newlineNow, multiply the result from Step 33 by the coefficient (49)(\frac{4}{9}).\newlinec(33)=(\frac{44}{99})\times 99
  5. Simplify the expression: Simplify the expression.\newlineSimplify the multiplication to find the 33rd term.\newlinec(3)=(49)∗9=4c(3)=\left(\frac{4}{9}\right)*9 = 4

More problems from Geometric sequences

Question
Find the sum of the finite arithmetic series. ∑n=110(7n+4)\sum_{n=1}^{10} (7n+4)\newline______
Get tutor helpright-arrow

Posted 6 months ago

Question
Type the missing number in this sequence: `55,\59,\63,\text{_____},\71,\75,\79`
Get tutor helpright-arrow

Posted 2 months ago

Question
Type the missing number in this sequence: `2, 4 8`, ______,`32`
Get tutor helpright-arrow

Posted 2 months ago

Question
What kind of sequence is this? 2,10,50,250,…2, 10, 50, 250, \ldots Choices:Choices:\newline[A]arithmetic\text{[A]arithmetic}\newline[B]geometric\text{[B]geometric}\newline[C]both\text{[C]both}\newline[D]neither\text{[D]neither}
Get tutor helpright-arrow

Posted 2 months ago

Question
What is the missing number in this pattern? 1,4,9,16,25,36,49,64,81,____1, 4, 9, 16, 25, 36, 49, 64, 81, \_\_\_\_
Get tutor helpright-arrow

Posted 5 months ago

Question
Classify the series. ∑n=012(n+2)3 \sum_{n = 0}^{12} (n + 2)^3 \newlineChoices:\newline[A]arithmetic\text{[A]arithmetic}\newline[B]geometric\text{[B]geometric}\newline[C]both\text{[C]both}\newline[D]neither\text{[D]neither}
Get tutor helpright-arrow

Posted 2 months ago

Question
Find the first three partial sums of the series.\newline1+6+11+16+21+26+⋯1 + 6 + 11 + 16 + 21 + 26 + \cdots\newlineWrite your answers as integers or fractions in simplest form.\newlineS1=S_1 = ____\newlineS2=S_2 = ____\newlineS3=S_3 = ____
Get tutor helpright-arrow

Posted 5 months ago

Question
Find the third partial sum of the series. \newline3+9+15+21+27+33+⋯3 + 9 + 15 + 21 + 27 + 33 + \cdots\newlineWrite your answer as an integer or a fraction in simplest form. \newlineS3=S_3 = ____
Get tutor helpright-arrow

Posted 5 months ago

Question
Find the first three partial sums of the series. \newline1+7+13+19+25+31+⋯1 + 7 + 13 + 19 + 25 + 31 + \cdots\newlineWrite your answers as integers or fractions in simplest form. \newlineS1=S_1 = ____\newlineS2=S_2 = ____\newlineS3=S_3 = ____
Get tutor helpright-arrow

Posted 6 months ago

Question
Does the infinite geometric series converge or diverge?\newline1+34+916+2764+⋯1 + \frac{3}{4} + \frac{9}{16} + \frac{27}{64} + \cdots\newlineChoices:\newline[A]converge\text{[A]converge}\newline[B]diverge\text{[B]diverge}
Get tutor helpright-arrow

Posted 2 months ago

View all (131)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant