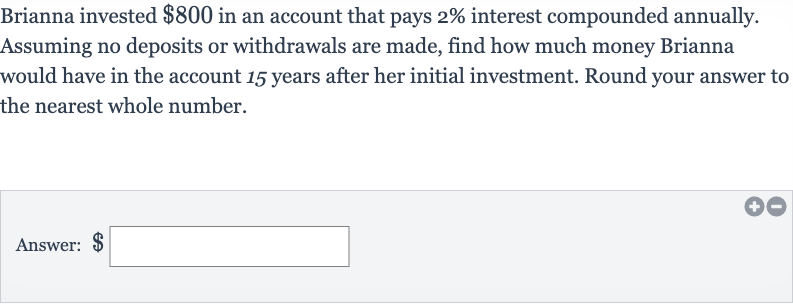
Brianna invested $800 in an account that pays 2% interest compounded annually. Assuming no deposits or withdrawals are made, find how much money Brianna would have in the account 15 years after her initial investment. Round your answer to the nearest whole number. Answer: $ □

Question

Brianna invested  $800 in an account that pays  2% interest compounded annually. Assuming no deposits or withdrawals are made, find how much money Brianna would have in the account 15 years after her initial investment. Round your answer to the nearest whole number. Answer:  $ □

Bytelearn · Accepted Answer

Given Information: We have: Initial investment (Principal, P): $800 Annual interest rate (r): 2% or 0.02 in decimal Number of years (t): 15 Interest is compounded annually (n): 1 time per year We will use the compound interest formula: A = P(1 + r/n)^(nt) Where A is the amount of money accumulated after n years, including interest. Let's calculate the amount A.Convert to Decimal: First, convert the interest rate from a percentage to a decimal by dividing by 100. Interest rate in decimal = 2% / 100 = 0.02Plug into Formula: Now, plug the values into the compound interest formula. A = 800(1 + 0.02/1)^(1*15)Simplify Expression: Simplify the expression inside the parentheses. A = 800(1 + 0.02)^15Add Numbers: Add the numbers inside the parentheses. A = 800(1.02)^15Calculate Value: Now, calculate the value of (1.02)^15. A = 800 * (1.02)^15 Using a calculator, (1.02)^15 ≈ 1.3498588075760032Multiply Principal: Multiply the principal amount by the calculated value. A = 800 * 1.3498588075760032 A ≈ 800 * 1.3499 (rounded to four decimal places for simplicity)Perform Multiplication: Now, perform the multiplication to find the total amount. A ≈ 800 * 1.3499 A ≈ 1079.92Round Answer: Round the answer to the nearest whole number as instructed. A ≈ $1080

Full solution

More problems from Compound interest

Related topics