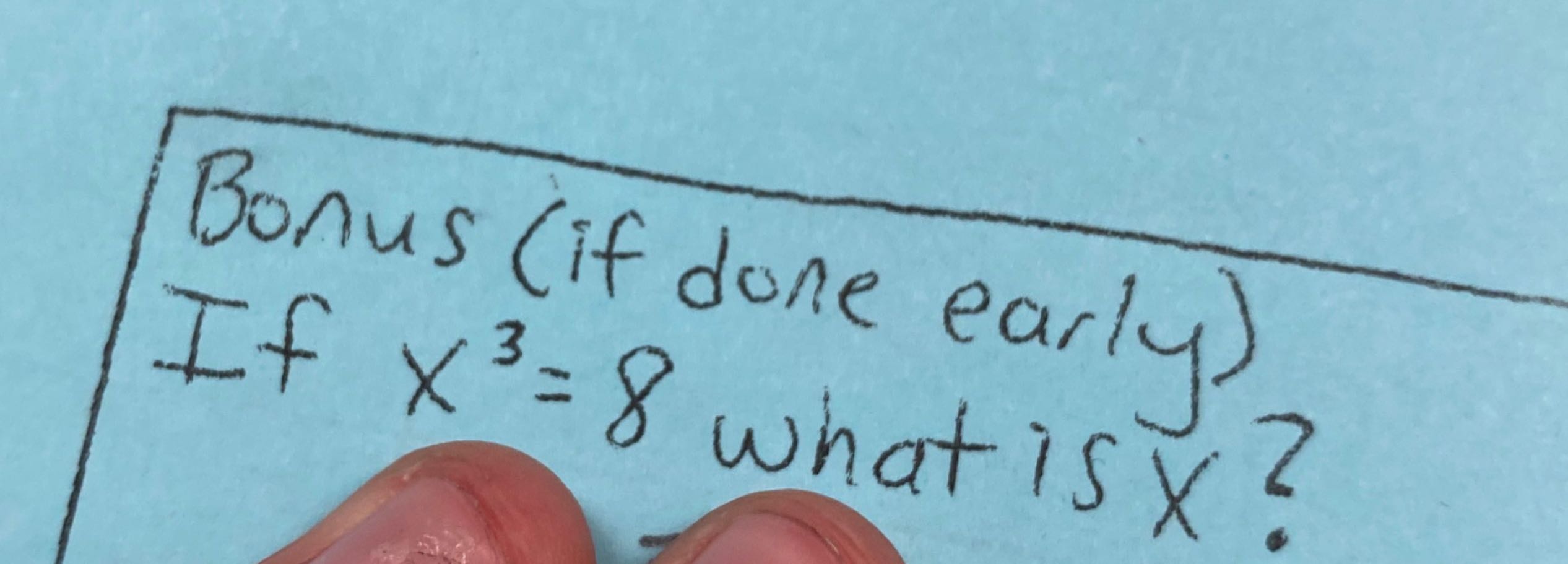Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Bonus (if done early)
If
x^(3)=8 what is
x ?

Bonus (if done early) $\newline$ If $x^{3}=8$ what is $x$ ?

View step-by-step help

View step-by-step help

Evaluate integers raised to positive rational exponents

Full solution

Q. Bonus (if done early)

\newline

If

x^{3}=8

what is

x

?

Identify Equation & Question: Identify the equation and what is being asked. $\newline$ We are given $x^{3}=8$ and need to find the value of $x$ .
Express $8$ as Term: Express $8$ as a term raised to the power of $3$ . $8$ is $2$ raised to the power of $3$ , since $2 \times 2 \times 2 = 8$ . So, we can write $8$ as $2^3$ .
Set Equation Equal: Set the equation $x^{3}$ equal to $2^{3}$ . $\newline$ Since $x^{3}=8$ and $8=2^{3}$ , we have $x^{3}=2^{3}$ .
Find Cube Root: Find the cube root of both sides of the equation. $\newline$ To find $x$ , we need to take the cube root of both sides of the equation because the cube root is the inverse operation of raising a number to the power of $3$ . $\newline$ The cube root of $x^{3}$ is $x$ , and the cube root of $2^3$ is $2$ . $\newline$ Therefore, $x = 2$ .

More problems from Evaluate integers raised to positive rational exponents

Question

\newline

81^{\frac{1}{2}}

\newline

Posted 2 months ago

Question

\newline

(-32)^{1/5}

\newline

Posted 2 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{w^{\frac{4}{3}}}{w^{\frac{7}{3}}}

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 2 months ago

Question

Simplify. Assume all variables are positive.

\newline

(2r^{\frac{1}{3}})^8

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 1 month ago

Question

Simplify. Assume all variables are positive.

\newline

v^{\frac{7}{4}} \cdot v^{\frac{9}{4}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 2 months ago

Question

\newline

1^{\frac{1}{4}} \cdot 1^{\frac{1}{4}}

\newline

Posted 1 month ago

Question

\newline

32^{(-1/5)}

Posted 1 month ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{w^{\frac{3}{2}}}{w^{\frac{5}{2}}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 2 months ago

Question

Simplify. Assume all variables are positive.

\newline

(27x)^{\frac{2}{3}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 2 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{x^{\frac{1}{4}}}{x^{\frac{11}{4}}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 1 month ago