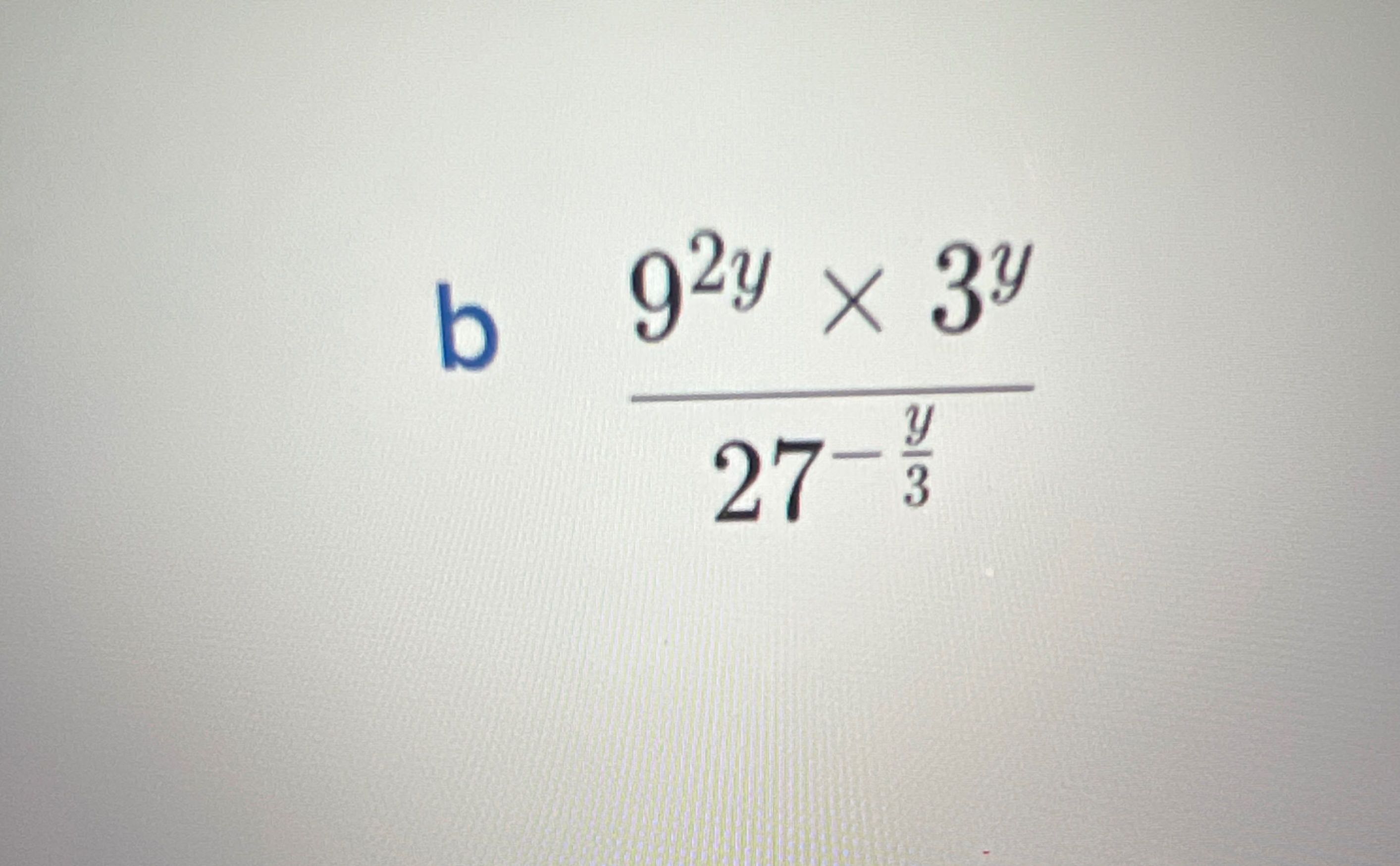AI tutor
Full solution
Q. Simplify.
- Express with same base: We start by expressing all the terms in the expression with the same base, which is , because and are both powers of . and
- Rewrite using base of : Rewrite the expression using the base of .=
- Apply power rules: Apply the power of a power rule and the power of a product rule . = =
- Combine exponents: Combine the exponents in the numerator using the power of a product rule.
- Apply quotient rule: Now we have: Apply the quotient of powers rule .
- Final simplified form: The expression is now simplified to: This is the final simplified form of the given expression.
More problems from Evaluate integers raised to rational exponents
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help