Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

ax+3y >= 7

2y <= ax+2
In the system of inequalities,
a is a constant. If
(1,2) is a solution to the system, which of the following is a possible value of
a ?
Choose 1 answer:
(A) -2
(B) -1
(C) 1
(D) 2

$a x+3 y \geq 7$ $\newline$ $2 y \leq a x+2$ $\newline$ In the system of inequalities, $a$ is a constant. If $(1,2)$ is a solution to the system, which of the following is a possible value of $a$ ? $\newline$ Choose $1$ answer: $\newline$ (A) $-2$ $\newline$ (B) $-1$ $\newline$ (C) $1$ $\newline$ (D) $2$

View step-by-step help

View step-by-step help

Is (x, y) a solution to the system of linear inequalities?

Full solution

Q.

a x+3 y \geq 7

\newline

2 y \leq a x+2

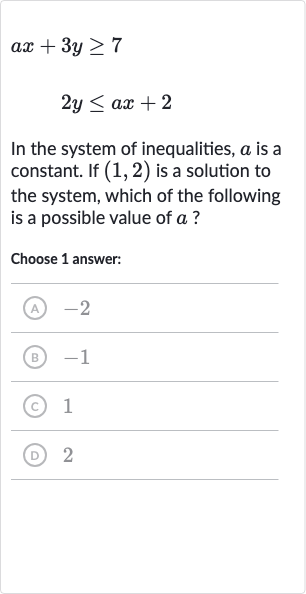
\newline

In the system of inequalities,

a

is a constant. If

(1,2)

is a solution to the system, which of the following is a possible value of

a

?

\newline

Choose

1

answer:

\newline

(A)

-2

\newline

(B)

-1

\newline

(C)

1

\newline

(D)

2

Substitute Point $(1,2)$ : Substitute the point $(1,2)$ into the first inequality $ax+3y \geq 7$ . $\newline$ Calculation: $a(1) + 3(2) \geq 7$ $\newline$ $a + 6 \geq 7$ $\newline$ $a \geq 7 - 6$ $\newline$ $a \geq 1$
Calculate First Inequality: Substitute the point $(1,2)$ into the second inequality $2y \leq ax+2$ . $\newline$ Calculation: $2(2) \leq a(1) + 2$ $\newline$ $4 \leq a + 2$ $\newline$ $a \geq 4 - 2$ $\newline$ $a \geq 2$
Calculate Second Inequality: Combine the results from both inequalities to find the possible values of $a$ . From the first inequality, we have $a \geq 1$ . From the second inequality, we have $a \geq 2$ . Therefore, $a$ must be greater than or equal to $2$ .

More problems from Is (x, y) a solution to the system of linear inequalities?

Question

Write the following inequality in slope-intercept form.

\newline

9x+y \geq -17

\newline

Write your answer with

y

first, followed by an inequality symbol. Use integers, proper fractions, and improper fractions in simplest form.

\newline

Posted 5 months ago

Question

(2,\,1)

make the inequality

2x + 15y < 20

\newline

\newline

\newline

Posted 5 months ago

Question

Jack is fixing up his home and must spend less than

\$4,800

to hire carpenters and painters. Carpenters charge

\$60

per hour and painters charge

\$32

\newline

Select the inequality in standard form that describes this situation. Use the given numbers and the following variables.

\newline

x =

the number of hours of carpentry

\newline

y =

the number of hours of painting

\newline

\newline

32x + 60y < 4,800

\newline

60x + 32y < 4,800

\newline

32x - 60y < 4,800

\newline

60x - 32y < 4,800

Posted 5 months ago

Question

(2,\, 10)

a solution to this system of inequalities?

\newline

y \geq x + 10

\newline

y \leq 9x + 5

\newline

\newline

\newline

Posted 5 months ago

Question

Write the following inequality in slope-intercept form.

\newline

4x - 2y \leq 8

\newline

Write your answer with

y

first, followed by an inequality symbol. Use integers, proper fractions, and improper fractions in simplest form.

Posted 9 months ago

Question

Write the following inequality in slope-intercept form.

\newline

-3x + 5y > 15

\newline

Write your answer with

y

first, followed by an inequality symbol. Use integers, proper fractions, and improper fractions in simplest form.

Posted 9 months ago

Question

Write the following inequality in slope-intercept form.

\newline

2x + 3y < -6

\newline

Write your answer with

y

first, followed by an inequality symbol. Use integers, proper fractions, and improper fractions in simplest form.

Posted 9 months ago

Question

Write the following inequality in slope-intercept form.

\newline

-7x - y \geq 21

\newline

Write your answer with

y

first, followed by an inequality symbol. Use integers, proper fractions, and improper fractions in simplest form.

Posted 8 months ago

Question

Write the following inequality in slope-intercept form.

\newline

5x - 4y > -20

\newline

Write your answer with

y

first, followed by an inequality symbol. Use integers, proper fractions, and improper fractions in simplest form.

Posted 9 months ago

Question

Miyoko's goal is to earn more than

(950

this week. She earns

)250

for every day she works as a cryptographer, and earns

\$180

for every day she works as a geologist.

\newline

Write an inequality that represents the number of days Miyoko should work as a cryptographer

C

and as a geologist

G

to achieve her goal.

Posted 10 months ago

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant