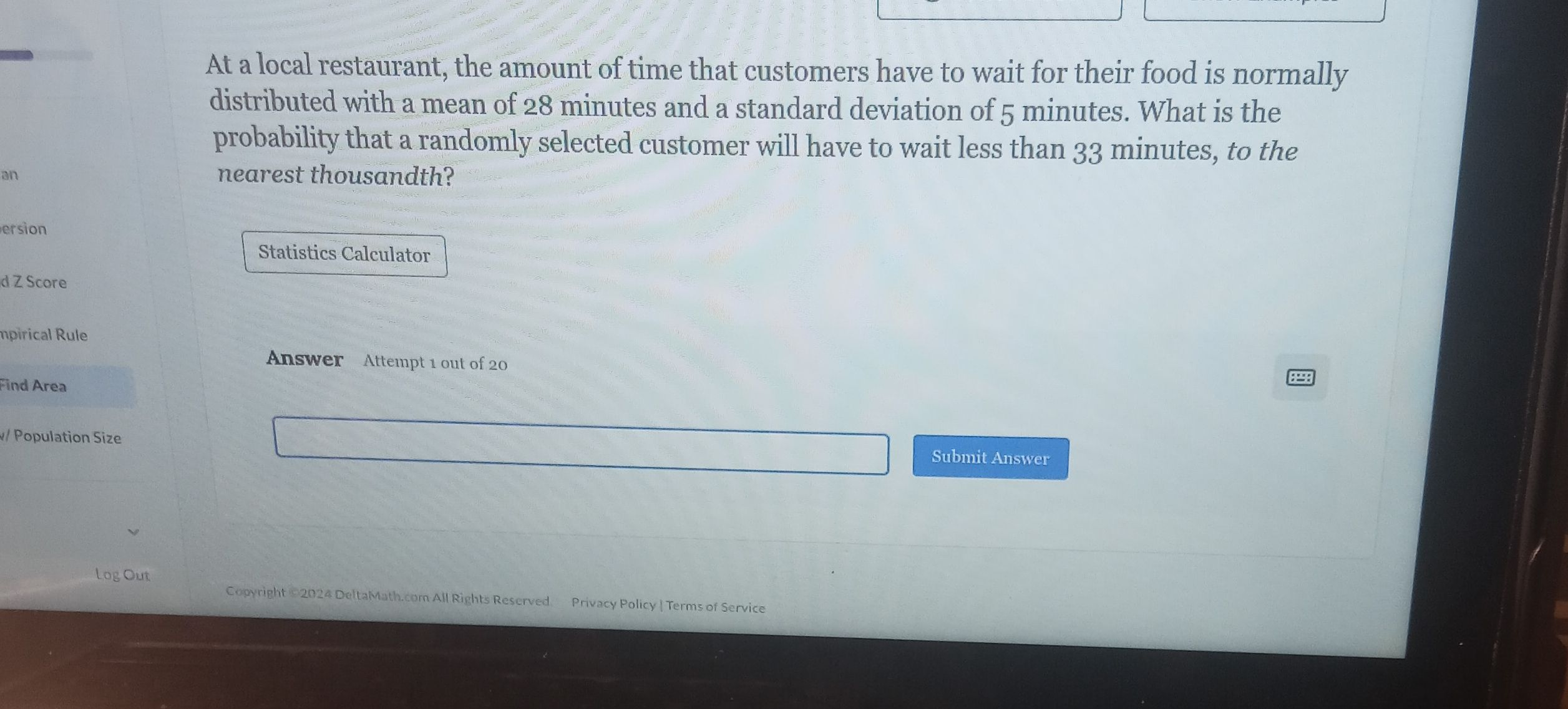
At a local restaurant, the amount of time that customers have to wait for their food is normally distributed with a mean of 28 minutes and a standard deviation of 5 minutes. What is the probability that a randomly selected customer will have to wait less than 33 minutes, to the nearest thousandth? Statistics Calculator Answer Attempt 1 out of 20 Nopulation Size Submit Answer Copyright 2024 Deltamath.com All Rights Reserved Privacy Policy / Terms of Service

Question

Bytelearn · Accepted Answer

Calculate z-score: To find the probability that a customer will have to wait less than 33 minutes, we need to calculate the z-score for 33 minutes using the mean and standard deviation provided. The formula for the z-score is: $$ z = \frac{(X - \mu)}{\sigma} $$ where $ X $ is the value we are looking at (33 minutes), $ \mu $ is the mean (28 minutes), and $ \sigma $ is the standard deviation (5 minutes).Find probability: Let's calculate the z-score for 33 minutes: $$ z = \frac{(33 - 28)}{5} $$ $$ z = \frac{5}{5} $$ $$ z = 1 $$ The z-score is 1.Use standard normal distribution: Now that we have the z-score, we can use the standard normal distribution table or a calculator to find the probability that a z-score is less than 1. The standard normal distribution table tells us the probability that a z-score is less than 1 is approximately 0.8413.Calculate final probability: Therefore, the probability that a randomly selected customer will have to wait less than 33 minutes is 0.8413, or to the nearest thousandth, 0.841.

Full solution

More problems from Interpret confidence intervals for population means

Related topics