Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Assuming
x and
y are both positive, write the following expression in simplest radical form.

3x^(2)y^(2)sqrt(28x^(5)y^(2))
Answer:

Assuming $x$ and $y$ are both positive, write the following expression in simplest radical form. $\newline$ $3 x^{2} y^{2} \sqrt{28 x^{5} y^{2}}$ $\newline$ Answer:

View step-by-step help

View step-by-step help

Simplify radical expressions with root inside the root

Full solution

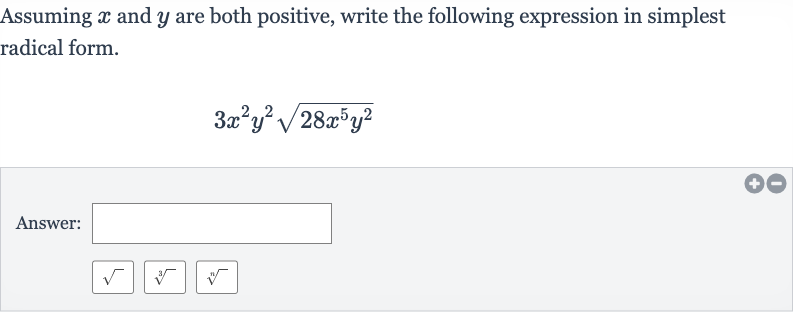
Q. Assuming

x

and

y

are both positive, write the following expression in simplest radical form.

\newline

3 x^{2} y^{2} \sqrt{28 x^{5} y^{2}}

\newline

Answer:

Write Expression and Identify Simplification: Write the given expression and identify the parts that can be simplified. $\newline$ The given expression is $3x^{2}y^{2}\sqrt{28x^{5}y^{2}}$ . We can simplify the square root by factoring out perfect squares.
Factor Expression to Identify Perfect Squares: Factor the expression inside the square root to identify perfect squares. $\sqrt{28x^{5}y^{2}}$ can be written as $\sqrt{4 \times 7 \times x^{4} \times x \times y^{2}}$ . We notice that $4$ , $x^{4}$ , and $y^{2}$ are perfect squares.
Take Perfect Squares out of Square Root: Take the perfect squares out of the square root. $\newline$ $\sqrt{4 \times 7 \times x^{4} \times x \times y^{2}} = \sqrt{4} \times \sqrt{x^{4}} \times \sqrt{y^{2}} \times \sqrt{7x}$ $\newline$ $= 2 \times x^{2} \times y \times \sqrt{7x}$ .
Multiply Simplified Square Root: Multiply the simplified square root with the rest of the given expression. $\newline$ Now we have $3x^{2}y^{2} \times (2 \times x^{2} \times y \times \sqrt{7x})$ $\newline$ = $3 \times 2 \times x^{2} \times x^{2} \times y^{2} \times y \times \sqrt{7x}$ $\newline$ = $6 \times x^{4} \times y^{3} \times \sqrt{7x}$ .
Write Final Simplified Expression: Write the final simplified expression. $\newline$ The expression $6 \times x^{4} \times y^{3} \times \sqrt{7x}$ is the simplest radical form of the given expression.

More problems from Simplify radical expressions with root inside the root

Question

Find the real-number root.

\newline

\sqrt{16}

\newline

\newline

Write your answer in simplified form.

\newline

\_\_\_\_

Posted 2 months ago

Question

Find the real-number root.

\newline

\sqrt{\frac{9}{16}}

\newline

Simplify your answer and write it as a decimal or as a proper or improper fraction.

\newline

\_\_\_\_\_

Posted 2 months ago

Question

Find the real-number root using a calculator. Round your answer to the nearest thousandth.

\newline

\newline

Posted 2 months ago

Question

Multiply. Write your answer in simplest form.

\newline

\sqrt{273} \times \sqrt{42}

\newline

Posted 1 month ago

Question

\newline

\sqrt{\frac{63}{4}}

\newline

Posted 2 months ago

Question

Simplify. Rationalize the denominator.

\newline

\frac{-4}{9 - \sqrt{2}}

\newline

Posted 2 months ago

Question

z

\newline

16 = \sqrt{z}

\newline

z =

Posted 2 months ago

Question

Simplify the radical expression.

\sqrt{14x^{14}}

Write your answer in the form

A

\sqrt{B}

A\sqrt{B}

A

B

are constants or expressions in

x

. Use at most one radical in your answer, and at most one absolute value symbol in your expression for

A

Posted 2 months ago

Question

Simplify the radical expression.

\newline

\sqrt{12x^{12}}

\newline

Write your answer in the form

A

\sqrt{B}

A\sqrt{B}

A

B

are constants or expressions in

x

. Use at most one radical in your answer, and at most one absolute value symbol in your expression for

A

\newline

\underline{\hspace{3cm}}

Posted 2 months ago

Question

What is the value of

\sin \left(\frac{5 \pi}{6}\right) ?

\newline

1

\newline

-\frac{\sqrt{3}}{2}

\newline

-\frac{\sqrt{2}}{2}

\newline

\frac{1}{2}

\newline

150

Posted 4 months ago