Full solution

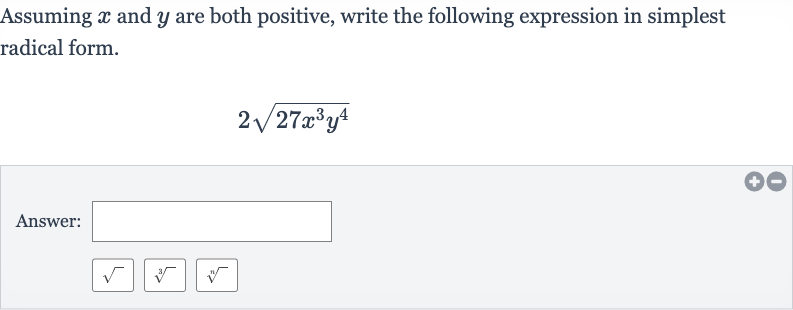
Q. Assuming

x

and

y

are both positive, write the following expression in simplest radical form.

\newline

2 \sqrt{27 x^{3} y^{4}}

\newline

Answer:

Break down radicand: Break down the radicand into prime factors and perfect squares. $\newline$ We have the expression $2\sqrt{27x^{3}y^{4}}$ . Let's first focus on the radicand (the number inside the square root), which is $27x^{3}y^{4}$ . We can break down $27$ into its prime factors and express $x^{3}$ and $y^{4}$ in a way that will help us simplify the square root. $\newline$ $27 = 3^{3}$ $\newline$ $x^{3}$ can be written as $x^{2} \times x$ , where $x^{2}$ is a perfect square. $\newline$ $y^{4}$ is already a perfect square since $27x^{3}y^{4}$ $0$ .
Simplify using perfect squares: Simplify the square root using the perfect squares. $\newline$ Now we can rewrite the radicand using the perfect squares we identified: $\newline$ $\sqrt{27x^{3}y^{4}} = \sqrt{(3^{3})(x^{2} \cdot x)(y^{4})}$ $\newline$ Since we know that $\sqrt{a^{2}} = a$ , we can take out the perfect squares from under the square root: $\newline$ $\sqrt{27x^{3}y^{4}} = \sqrt{(3^{2} \cdot 3)(x^{2})(y^{2})^{2}}$ $\newline$ $= \sqrt{9 \cdot 3 \cdot x^{2} \cdot y^{4}}$ $\newline$ $= \sqrt{9} \cdot \sqrt{3} \cdot \sqrt{x^{2}} \cdot \sqrt{y^{4}}$ $\newline$ $= 3 \cdot \sqrt{3} \cdot x \cdot y^{2}$
Multiply by coefficient: Multiply the simplified square root by the coefficient outside the square root. We now have the simplified square root, which we need to multiply by the coefficient $2$ that is outside the square root in the original expression: $2 \times (3 \times \sqrt{3} \times x \times y^{2}) = 6 \times \sqrt{3} \times x \times y^{2}$