Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Assuming
x and
y are both positive, write the following expression in simplest radical form.

4x^(2)y^(3)sqrt(27x^(2)y^(7))
Answer:

Assuming $x$ and $y$ are both positive, write the following expression in simplest radical form. $\newline$ $4 x^{2} y^{3} \sqrt{27 x^{2} y^{7}}$ $\newline$ Answer:

View step-by-step help

View step-by-step help

Simplify radical expressions with root inside the root

Full solution

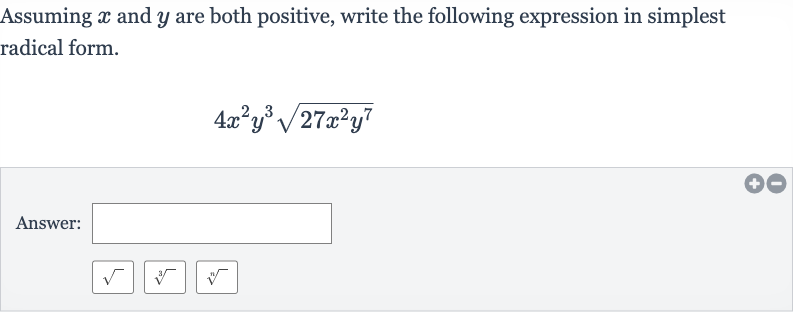
Q. Assuming

x

and

y

are both positive, write the following expression in simplest radical form.

\newline

4 x^{2} y^{3} \sqrt{27 x^{2} y^{7}}

\newline

Answer:

Write Expression: Write the given expression and identify the parts that can be simplified. $\newline$ The given expression is $4x^{2}y^{3}\sqrt{27x^{2}y^{7}}$ . $\newline$ We can simplify the square root part by factoring out perfect squares.
Factor Inside Square Root: Factor the expression inside the square root to identify perfect squares. $\newline$ The expression inside the square root is $27x^{2}y^{7}$ . $\newline$ $27$ is a perfect cube ( $3^{3}$ ), $x^{2}$ is already a perfect square, and $y^{7}$ can be written as $(y^{6}\cdot y)$ , where $y^{6}$ is a perfect square.
Take Out Perfect Squares: Take out the perfect squares from under the square root. $\newline$ $\sqrt{27x^{2}y^{7}} = \sqrt{3^{3} \times x^{2} \times y^{6} \times y}$ $\newline$ = $\sqrt{3^{2} \times 3 \times x^{2} \times y^{6}} \times \sqrt{y}$ $\newline$ = $3xy^{3} \times \sqrt{3y}$
Multiply Simplified Square Root: Multiply the simplified square root by the rest of the given expression. $\newline$ Now we have $4x^{2}y^{3} \times 3xy^3 \times \sqrt{3y}$ . $\newline$ Multiplying the coefficients (numbers in front of the variables) gives us $4 \times 3 = 12$ . $\newline$ Multiplying the variables with the same base, we add the exponents: $x^{2+1} = x^3$ and $y^{3+3} = y^6$ .
Write Final Expression: Write the final simplified expression. $\newline$ The final expression is $12x^3y^6 \cdot \sqrt{3y}$ .

More problems from Simplify radical expressions with root inside the root

Question

Find the real-number root.

\newline

\sqrt{16}

\newline

\newline

Write your answer in simplified form.

\newline

\_\_\_\_

Posted 2 months ago

Question

Find the real-number root.

\newline

\sqrt{\frac{9}{16}}

\newline

Simplify your answer and write it as a decimal or as a proper or improper fraction.

\newline

\_\_\_\_\_

Posted 2 months ago

Question

Find the real-number root using a calculator. Round your answer to the nearest thousandth.

\newline

\newline

Posted 2 months ago

Question

Multiply. Write your answer in simplest form.

\newline

\sqrt{273} \times \sqrt{42}

\newline

Posted 1 month ago

Question

\newline

\sqrt{\frac{63}{4}}

\newline

Posted 2 months ago

Question

Simplify. Rationalize the denominator.

\newline

\frac{-4}{9 - \sqrt{2}}

\newline

Posted 2 months ago

Question

z

\newline

16 = \sqrt{z}

\newline

z =

Posted 2 months ago

Question

Simplify the radical expression.

\sqrt{14x^{14}}

Write your answer in the form

A

\sqrt{B}

A\sqrt{B}

A

B

are constants or expressions in

x

. Use at most one radical in your answer, and at most one absolute value symbol in your expression for

A

Posted 2 months ago

Question

Simplify the radical expression.

\newline

\sqrt{12x^{12}}

\newline

Write your answer in the form

A

\sqrt{B}

A\sqrt{B}

A

B

are constants or expressions in

x

. Use at most one radical in your answer, and at most one absolute value symbol in your expression for

A

\newline

\underline{\hspace{3cm}}

Posted 2 months ago

Question

What is the value of

\sin \left(\frac{5 \pi}{6}\right) ?

\newline

1

\newline

-\frac{\sqrt{3}}{2}

\newline

-\frac{\sqrt{2}}{2}

\newline

\frac{1}{2}

\newline

150

Posted 4 months ago