Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Assuming
x and
y are both positive, write the following expression in simplest radical form.

7xsqrt(9x^(2)y^(4))
Answer:

Assuming $x$ and $y$ are both positive, write the following expression in simplest radical form. $\newline$ $7 x \sqrt{9 x^{2} y^{4}}$ $\newline$ Answer:

View step-by-step help

View step-by-step help

Simplify radical expressions with variables II

Full solution

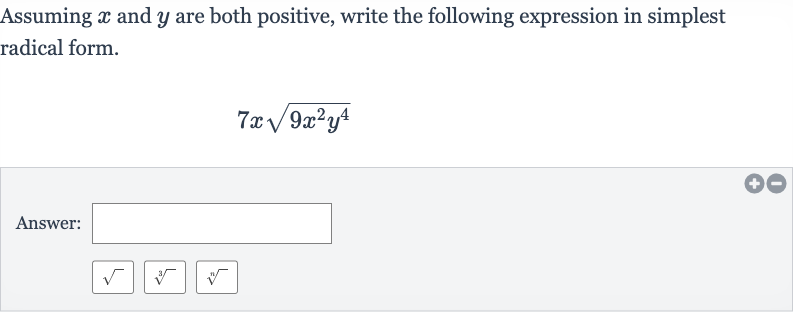
Q. Assuming

x

and

y

are both positive, write the following expression in simplest radical form.

\newline

7 x \sqrt{9 x^{2} y^{4}}

\newline

Answer:

Simplify Inside Radical: Simplify the square root of the constant and variables inside the radical. $\newline$ We have the expression $7x\sqrt{9x^2y^4}$ . Let's first focus on the constant and variables inside the radical. $\newline$ The square root of $9$ is $3$ , because $3^2 = 9$ . $\newline$ The square root of $x^2$ is $x$ , because $(x)^2 = x^2$ . $\newline$ The square root of $y^4$ is $y^2$ , because $(y^2)^2 = y^4$ . $\newline$ So, $9$ $0$ .
Multiply by Coefficient: Multiply the simplified radical by the coefficient outside the radical. $\newline$ Now we have $7x \times 3xy^2$ . $\newline$ Multiplying the coefficients ( $7$ and $3$ ) and the variables ( $x$ and $xy^2$ ) gives us $21x^2y^2$ .

More problems from Simplify radical expressions with variables II

Question

Find the real-number root.

\newline

\sqrt{16}

\newline

\newline

Write your answer in simplified form.

\newline

\_\_\_\_

Posted 2 months ago

Question

Find the real-number root.

\newline

\sqrt{\frac{9}{16}}

\newline

Simplify your answer and write it as a decimal or as a proper or improper fraction.

\newline

\_\_\_\_\_

Posted 2 months ago

Question

Find the real-number root using a calculator. Round your answer to the nearest thousandth.

\newline

\newline

Posted 2 months ago

Question

Multiply. Write your answer in simplest form.

\newline

\sqrt{273} \times \sqrt{42}

\newline

Posted 1 month ago

Question

\newline

\sqrt{\frac{63}{4}}

\newline

Posted 2 months ago

Question

Simplify. Rationalize the denominator.

\newline

\frac{-4}{9 - \sqrt{2}}

\newline

Posted 2 months ago

Question

z

\newline

16 = \sqrt{z}

\newline

z =

Posted 2 months ago

Question

Simplify the radical expression.

\sqrt{14x^{14}}

Write your answer in the form

A

\sqrt{B}

A\sqrt{B}

A

B

are constants or expressions in

x

. Use at most one radical in your answer, and at most one absolute value symbol in your expression for

A

Posted 2 months ago

Question

Simplify the radical expression.

\newline

\sqrt{12x^{12}}

\newline

Write your answer in the form

A

\sqrt{B}

A\sqrt{B}

A

B

are constants or expressions in

x

. Use at most one radical in your answer, and at most one absolute value symbol in your expression for

A

\newline

\underline{\hspace{3cm}}

Posted 2 months ago

Question

What is the value of

\sin \left(\frac{5 \pi}{6}\right) ?

\newline

1

\newline

-\frac{\sqrt{3}}{2}

\newline

-\frac{\sqrt{2}}{2}

\newline

\frac{1}{2}

\newline

150

Posted 4 months ago