AI tutor
Welcome to Bytelearn!
Let’s check out your problem:
Assuming and are both positive, write the following expression in simplest radical form.Answer:
Full solution
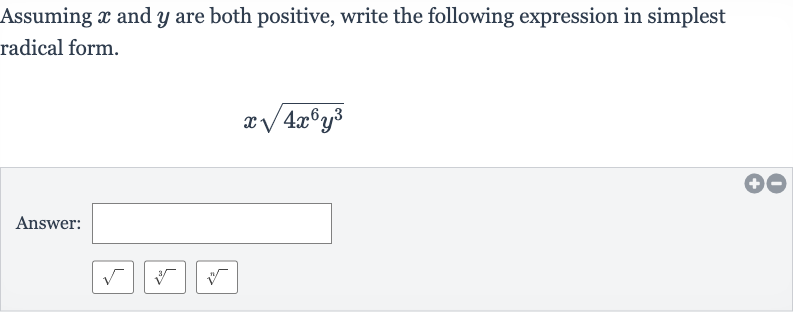
Q. Assuming and are both positive, write the following expression in simplest radical form.Answer:
- Simplify constant term: Simplify the square root of the constant term.The constant term inside the square root is , which is a perfect square (). We can take the square root of out of the radical.
- Simplify variable term : Simplify the square root of the variable term . Since is a perfect square , we can take out of the radical.
- Simplify variable term : Simplify the square root of the variable term . We cannot take the entire out of the radical because it is not a perfect square. However, we can separate it into , where is a perfect square and can be taken out of the radical.
- Combine results: Combine the results from steps , , and . We multiply the terms that came out of the radical together with the original that was outside the radical.
