Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Assuming
x and
y are both positive, write the following expression in simplest radical form.

7y^(3)sqrt(36x^(6)y^(5))
Answer:

Assuming $x$ and $y$ are both positive, write the following expression in simplest radical form. $\newline$ $7 y^{3} \sqrt{36 x^{6} y^{5}}$ $\newline$ Answer:

View step-by-step help

View step-by-step help

Simplify radical expressions with root inside the root

Full solution

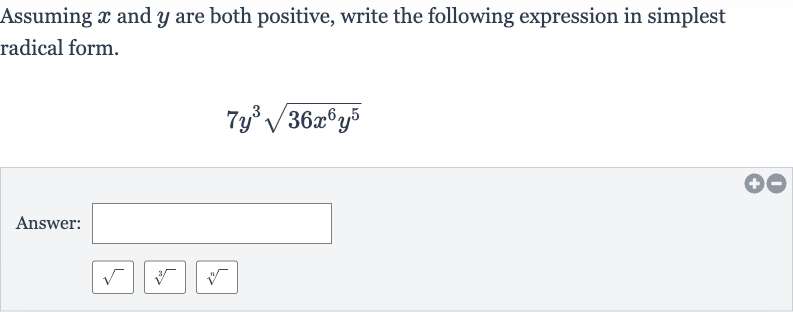
Q. Assuming

x

and

y

are both positive, write the following expression in simplest radical form.

\newline

7 y^{3} \sqrt{36 x^{6} y^{5}}

\newline

Answer:

Simplify Square Root of $36$ : Simplify the square root of $36$ . $\newline$ The square root of $36$ is $6$ because $6^2 = 36$ .
Simplify Square Root of $x^{6}$ : Simplify the square root of $x^{6}$ . Since $x$ is positive and the exponent $6$ is even, $\sqrt{x^{6}}$ is $x^{6/2} = x^{3}$ .
Simplify Square Root of $y^{5}$ : Simplify the square root of $y^{5}$ . We can split $y^{5}$ into $y^{4}\cdot y^{1}$ . The square root of $y^{4}$ is $y^{\frac{4}{2}} = y^{2}$ , and the square root of $y^{1}$ remains under the radical as $\sqrt{y}$ .
Combine Simplified Parts: Combine the simplified parts outside the radical. $\newline$ We have $7y^{3} \times 6 \times x^{3} \times y^{2}$ from the previous steps. $\newline$ Multiplying these together gives us $42y^{3} \times x^{3} \times y^{2}$ .
Combine Like Terms: Combine the like terms. $\newline$ $y^{3} \times y^{2}$ can be combined by adding the exponents since they have the same base. $\newline$ This gives us $y^{3+2} = y^{5}$ . $\newline$ So, we have $42 \times x^{3} \times y^{5}$ .
Combine Simplified Parts Inside Radical: Combine the simplified parts inside the radical. We are left with $\sqrt{y}$ inside the radical.
Write Final Expression: Write the final expression. $\newline$ The final expression is $42x^{3}y^{5}\sqrt{y}$ .

More problems from Simplify radical expressions with root inside the root

Question

Find the real-number root.

\newline

\sqrt{16}

\newline

\newline

Write your answer in simplified form.

\newline

\_\_\_\_

Posted 2 months ago

Question

Find the real-number root.

\newline

\sqrt{\frac{9}{16}}

\newline

Simplify your answer and write it as a decimal or as a proper or improper fraction.

\newline

\_\_\_\_\_

Posted 2 months ago

Question

Find the real-number root using a calculator. Round your answer to the nearest thousandth.

\newline

\newline

Posted 2 months ago

Question

Multiply. Write your answer in simplest form.

\newline

\sqrt{273} \times \sqrt{42}

\newline

Posted 1 month ago

Question

\newline

\sqrt{\frac{63}{4}}

\newline

Posted 2 months ago

Question

Simplify. Rationalize the denominator.

\newline

\frac{-4}{9 - \sqrt{2}}

\newline

Posted 2 months ago

Question

z

\newline

16 = \sqrt{z}

\newline

z =

Posted 2 months ago

Question

Simplify the radical expression.

\sqrt{14x^{14}}

Write your answer in the form

A

\sqrt{B}

A\sqrt{B}

A

B

are constants or expressions in

x

. Use at most one radical in your answer, and at most one absolute value symbol in your expression for

A

Posted 2 months ago

Question

Simplify the radical expression.

\newline

\sqrt{12x^{12}}

\newline

Write your answer in the form

A

\sqrt{B}

A\sqrt{B}

A

B

are constants or expressions in

x

. Use at most one radical in your answer, and at most one absolute value symbol in your expression for

A

\newline

\underline{\hspace{3cm}}

Posted 2 months ago

Question

What is the value of

\sin \left(\frac{5 \pi}{6}\right) ?

\newline

1

\newline

-\frac{\sqrt{3}}{2}

\newline

-\frac{\sqrt{2}}{2}

\newline

\frac{1}{2}

\newline

150

Posted 4 months ago