AI tutor
Welcome to Bytelearn!
Let’s check out your problem:
Assuming and are both positive, write the following expression in simplest radical form.Answer:
Full solution
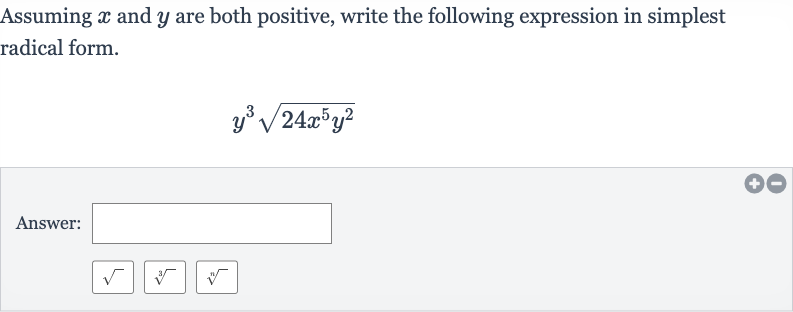
Q. Assuming and are both positive, write the following expression in simplest radical form.Answer:
- Express in Exponential Form: First, let's express the square root in exponential form and combine the exponents that are outside and inside the radical.=
- Apply Power Rules: Now, we apply the power to a product rule and the power to a power rule to the expression inside the radical.= * * =
- Multiply by : Next, we multiply the expression we just found by outside the radical.y^{3} \times 2 \times \sqrt{6} \times x^{\frac{5}{2}} \times y\(\newline= 2y^{3} \times \sqrt{6} \times x^{\frac{5}{2}} \times y\)
- Combine Y Terms: We can now combine the y terms by adding the exponents, since they have the same base.2y^{3} \cdot \sqrt{6} \cdot x^{\frac{5}{2}} \cdot y\(\newline= 2y^{3+1} \cdot \sqrt{6} \cdot x^{\frac{5}{2}}= 2y^{4} \cdot \sqrt{6} \cdot x^{\frac{5}{2}}\)
- Final Simplification: Finally, we write the expression in its simplest radical form.This is the simplest radical form because there are no like terms to combine and no further simplification of the radical is possible.
