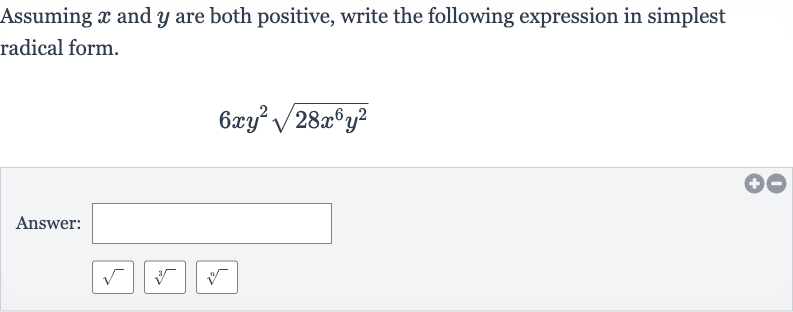
Assuming x and y are both positive, write the following expression in simplest radical form. 6xy^(2)sqrt(28x^(6)y^(2)) Answer:

Question

Assuming  x and  y are both positive, write the following expression in simplest radical form.  6xy^(2)sqrt(28x^(6)y^(2)) Answer:

Bytelearn · Accepted Answer

Factor and Separate Perfect Squares: Factor the expression inside the square root to separate perfect squares from non-perfect squares. sqrt(28x^(6)y^(2)) can be factored into sqrt(4 * 7 * x^(6) * y^(2)). 4 and x^(6) are perfect squares, so they can be taken out of the square root. sqrt(4 * 7 * x^(6) * y^(2)) = sqrt(4) * sqrt(x^(6)) * sqrt(7) * sqrt(y^(2))Simplify Perfect Squares: Simplify the square roots of the perfect squares. sqrt(4) = 2, sqrt(x^(6)) = x^(3), and sqrt(y^(2)) = y because x and y are positive. So, we have 2 * x^(3) * y * sqrt(7).Multiply by Outside Term: Multiply the simplified square roots by the outside term 6xy^(2). 6xy^(2) * (2 * x^(3) * y * sqrt(7)) = 6 * 2 * x * x^(3) * y^(2) * y * sqrt(7)Combine Like Terms: Combine like terms by adding the exponents for x and y. 6 * 2 = 12, x * x^(3) = x^(1+3) = x^(4), y^(2) * y = y^(2+1) = y^(3). So, we have 12 * x^(4) * y^(3) * sqrt(7).Write Final Expression: Write the final simplified expression. The expression in simplest radical form is 12x^(4)y^(3)sqrt(7).

Assuming $x$ and $y$ are both positive, write the following expression in simplest radical form. $\newline$ $6 x y^{2} \sqrt{28 x^{6} y^{2}}$ $\newline$ Answer:

Full solution

More problems from Evaluate rational expressions II

Related topics

Assuming x x x and y y y are both positive, write the following expression in simplest radical form.\newline6xy228x6y2 6 x y^{2} \sqrt{28 x^{6} y^{2}} 6xy228x6y2​\newlineAnswer:

Assuming $x$ and $y$ are both positive, write the following expression in simplest radical form. $\newline$ $6 x y^{2} \sqrt{28 x^{6} y^{2}}$ $\newline$ Answer: