Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Assuming that x is in the appropriate domain, find a formula for h^(-1)(x)=1-(sin^(-1)(((-8-x))/(2)))

Assuming that x x is in the appropriate domain, find a formula for\newlineh−1(x)=1−(sin⁡−1((−8−x)2)) h^{-1}(x)=1-\left(\sin ^{-1}\left(\frac{(-8-x)}{2}\right)\right)

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 1right chevron icon
Evaluate integers raised to rational exponentsright chevron icon

Full solution

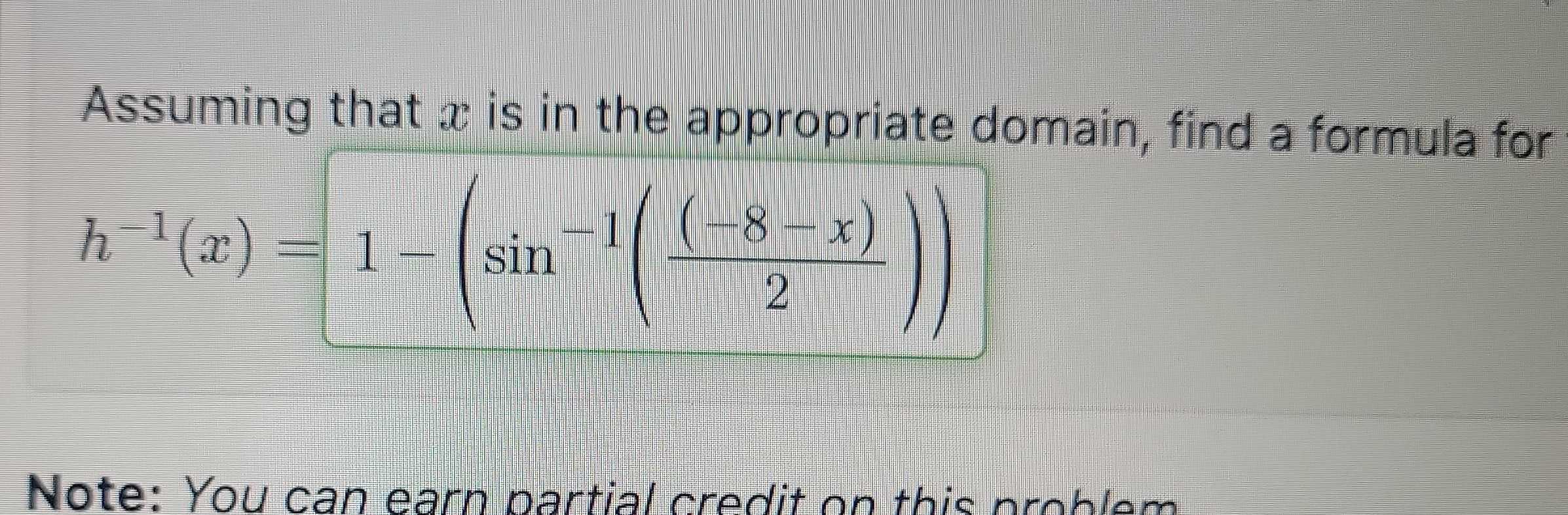
Q. Assuming that x x is in the appropriate domain, find a formula for\newlineh−1(x)=1−(sin⁡−1((−8−x)2)) h^{-1}(x)=1-\left(\sin ^{-1}\left(\frac{(-8-x)}{2}\right)\right)
  1. Start with given equation: To find the formula for the inverse function h−1(x)h^{-1}(x), we need to express xx in terms of hh. We start with the given equation for h−1(x)h^{-1}(x):\newlineh−1(x)=1−sin⁡−1(−8−x2)h^{-1}(x) = 1 - \sin^{-1}\left(\frac{-8 - x}{2}\right)\newlineLet's denote h−1(x)h^{-1}(x) as yy for simplicity:\newliney=1−sin⁡−1(−8−x2)y = 1 - \sin^{-1}\left(\frac{-8 - x}{2}\right)
  2. Isolate sin⁡−1\sin^{-1} term: Now we need to solve for xx. First, we isolate the sin⁡−1\sin^{-1} term by moving everything else to the other side of the equation:\newlinesin⁡−1(−8−x2)=1−y\sin^{-1}\left(\frac{-8 - x}{2}\right) = 1 - y
  3. Apply sine function: Next, we apply the sine function to both sides to remove the inverse sine, keeping in mind that sin⁡(sin⁡−1(u))=u\sin(\sin^{-1}(u)) = u for all uu in the domain of sin⁡−1\sin^{-1}:sin⁡(sin⁡−1(−8−x2))=sin⁡(1−y)\sin(\sin^{-1}(\frac{-8 - x}{2})) = \sin(1 - y)−8−x2=sin⁡(1−y)\frac{-8 - x}{2} = \sin(1 - y)
  4. Multiply by 22: Now we multiply both sides by 22 to get rid of the denominator:\newline−8−x=2sin⁡(1−y)-8 - x = 2\sin(1 - y)
  5. Isolate xx: Next, we isolate xx by moving the −8-8 to the other side:\newline−x=2sin⁡(1−y)+8-x = 2\sin(1 - y) + 8
  6. Multiply by −1-1: Finally, we multiply both sides by −1-1 to solve for xx:x=−2sin⁡(1−y)−8x = -2\sin(1 - y) - 8
  7. Replace yy with h−1(x)h^{-1}(x): Now we replace yy with h−1(x)h^{-1}(x) to get the formula for the inverse function in terms of xx:
    x=−2sin⁡(1−h−1(x))−8x = -2\sin(1 - h^{-1}(x)) - 8
    However, this is not quite correct because we need to express h−1(x)h^{-1}(x) in terms of xx, not the other way around. We need to go back and correct this mistake.

More problems from Evaluate integers raised to rational exponents

Question
Simplify.\newline811281^{\frac{1}{2}}\newline_____________
Get tutor helpright-arrow

Posted 9 months ago

Question
Simplify.\newline(−32)1/5(-32)^{1/5}\newline______
Get tutor helpright-arrow

Posted 9 months ago

Question
Simplify. Assume all variables are positive.\newlinew43w73\frac{w^{\frac{4}{3}}}{w^{\frac{7}{3}}}\newlineWrite your answer in the form AA or AB\frac{A}{B}, where AA and BB are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.\newline______
Get tutor helpright-arrow

Posted 5 months ago

Question
Simplify. Assume all variables are positive.\newline(2r13)8(2r^{\frac{1}{3}})^8\newline\newlineWrite your answer in the form AA or AB\frac{A}{B}, where AA and BB are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.\newline______
Get tutor helpright-arrow

Posted 5 months ago

Question
Simplify. Assume all variables are positive.\newlinev74⋅v94v^{\frac{7}{4}} \cdot v^{\frac{9}{4}}\newline\newlineWrite your answer in the form AA or AB\frac{A}{B}, where AA and BB are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.\newline______\newline
Get tutor helpright-arrow

Posted 5 months ago

Question
Simplify.\newline114⋅1141^{\frac{1}{4}} \cdot 1^{\frac{1}{4}}\newline______
Get tutor helpright-arrow

Posted 5 months ago

Question
Simplify. \newline32(−1/5)32^{(-1/5)}
Get tutor helpright-arrow

Posted 7 months ago

Question
Simplify. Assume all variables are positive.\newlinew32w52\frac{w^{\frac{3}{2}}}{w^{\frac{5}{2}}}\newline\newlineWrite your answer in the form AA or AB\frac{A}{B}, where AA and BB are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.\newline______\newline
Get tutor helpright-arrow

Posted 9 months ago

Question
Simplify. Assume all variables are positive.\newline(27x)23(27x)^{\frac{2}{3}}\newline\newlineWrite your answer in the form AA or AB\frac{A}{B}, where AA and BB are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.\newline______
Get tutor helpright-arrow

Posted 8 months ago

Question
Simplify. Assume all variables are positive.\newlinex14x114\frac{x^{\frac{1}{4}}}{x^{\frac{11}{4}}}\newline\newlineWrite your answer in the form AA or AB\frac{A}{B}, where AA and BB are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.\newline______\newline
Get tutor helpright-arrow

Posted 7 months ago

View all (95)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant