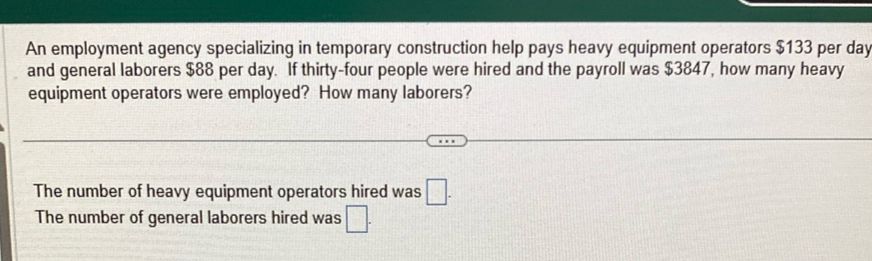
An employment agency specializing in temporary construction help pays heavy equipment operators $133 per day and general laborers $88 per day. If thirty-four people were hired and the payroll was $3847, how many heavy equipment operators were employed? How many laborers? The number of heavy equipment operators hired was ◻ The number of general laborers hired was ◻

Question

An employment agency specializing in temporary construction help pays heavy equipment operators  $133 per day and general laborers  $88 per day. If thirty-four people were hired and the payroll was  $3847, how many heavy equipment operators were employed? How many laborers? The number of heavy equipment operators hired was  ◻ The number of general laborers hired was  ◻

Bytelearn · Accepted Answer

Define Variables:  Let x be the number of heavy equipment operators and y be the number of general laborers. We know that x + y = 34 (total people hired). Form Equations:  We also know that 133x + 88y = 3847 (total payroll). Solve for y:  Solve for y in the first equation: y = 34 - x. Substitute y:  Substitute y in the second equation: 133x + 88(34 - x) = 3847. Simplify Equation:  Simplify the equation: 133x + 2992 - 88x = 3847. Combine Like Terms:  Combine like terms: 45x + 2992 = 3847. Solve for x:  Solve for x: 45x = 3847 - 2992. Calculate x:  Calculate x: 45x = 855. Divide by 45:  Divide by 45: x = 855 / 45. Calculate x:  x = 19. So, 19 heavy equipment operators were employed. Substitute x:  Substitute x back into the equation for y: y = 34 - 19. Calculate y:  y = 15. So, 15 general laborers were employed.

Full solution

More problems from Multi-step word problems

Related topics