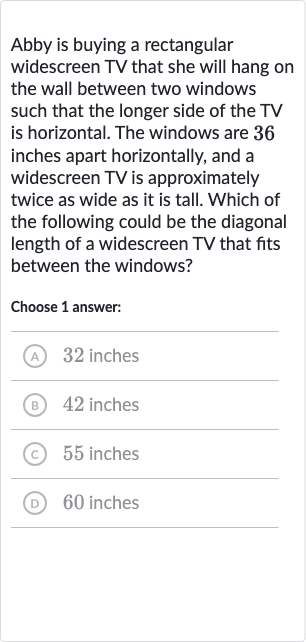
Abby is buying a rectangular widescreen TV that she will hang on the wall between two windows such that the longer side of the TV is horizontal. The windows are 36 inches apart horizontally, and a widescreen TV is approximately twice as wide as it is tall. Which of the following could be the diagonal length of a widescreen TV that fits between the windows? Choose 1 answer: A) 32 inches (B) 42 inches (C) 55 inches (D) 60 inches

Question

Bytelearn · Accepted Answer

Calculate TV Width: Determine the maximum width of the TV that can fit between the windows. Since the windows are 36 inches apart, the TV width must be less than 36 inches to fit.Aspect Ratio for Height: Use the aspect ratio of the widescreen TV to find the height. A widescreen TV is approximately twice as wide as it is tall. Let's denote the width as 2h and the height as h, where h is the height of the TV.Inequality for Height: Since the width must be less than 36 inches, set up the inequality 2h < 36. Solve for h to find the maximum height of the TV. 2h < 36 h < 36 / 2 h < 18 The height of the TV must be less than 18 inches.Pythagorean Theorem: Use the Pythagorean Theorem to find the diagonal length of the TV. The Pythagorean Theorem states that in a right-angled triangle, the square of the length of the hypotenuse (c) is equal to the sum of the squares of the lengths of the other two sides (a and b). c^2 = a^2 + b^2 Here, a = h and b = 2h, so we have: c^2 = h^2 + (2h)^2 c^2 = h^2 + 4h^2 c^2 = 5h^2Calculate Diagonal Length: Since h must be less than 18 inches, find the maximum diagonal length using h = 18. c^2 = 5h^2 c^2 = 5(18)^2 c^2 = 5(324) c^2 = 1620 c = sqrt(1620) c ≈ 40.25 inchesComparison with Options: Compare the calculated diagonal length with the given options. The calculated diagonal length of approximately 40.25 inches is closest to option (B) 42 inches. However, since the TV must fit between the windows, we must choose a diagonal length that is less than or equal to 40.25 inches.Choose Correct Answer: Choose the correct answer based on the options provided. Option (A) 32 inches is the only diagonal length that is less than 40.25 inches and can fit between the windows.

Full solution

More problems from Pythagorean Theorem and its converse

Related topics