Full solution
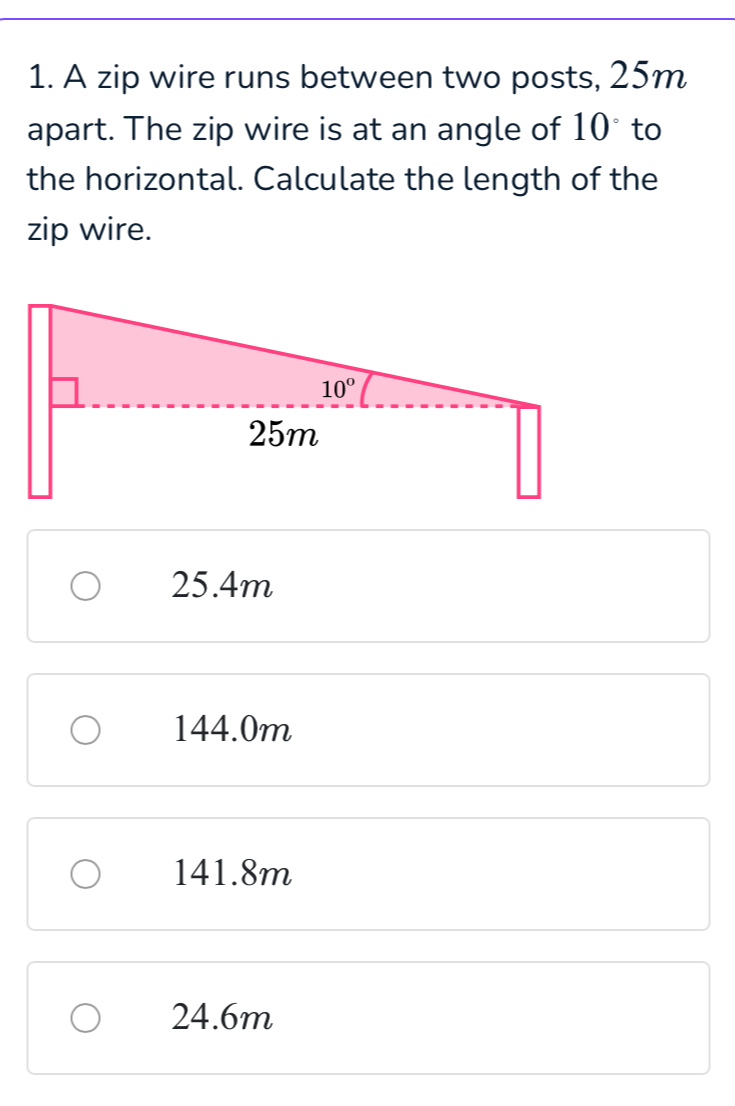
Q. . A zip wire runs between two posts, apart. The zip wire is at an angle of to the horizontal. Calculate the length of the zip wire.
- Identify values and equation: Identify the known values and the equation to use.We know the distance between the two posts (the adjacent side of the right triangle) is meters, and the angle of elevation is degrees. We need to find the length of the zip wire, which is the hypotenuse of the right triangle.We will use the cosine function, which relates the adjacent side and hypotenuse of a right triangle to the angle: .
- Use cosine function: Use the cosine function to set up the equation.We need to solve for the .
- Rearrange for hypotenuse: Rearrange the equation to solve for the hypotenuse.hypotenuse Now we can calculate the length of the hypotenuse using a calculator.
- Calculate hypotenuse: Calculate the length of the hypotenuse using a calculator.hypotenuse hypotenuse (cosine of degrees is approximately )hypotenuse
More problems from Pythagorean Theorem and its converse
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
Question
. Find the value of in degrees.Write your answer in simplified, rationalized form. Do not round.____
Get tutor helpQuestionGet tutor help