Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

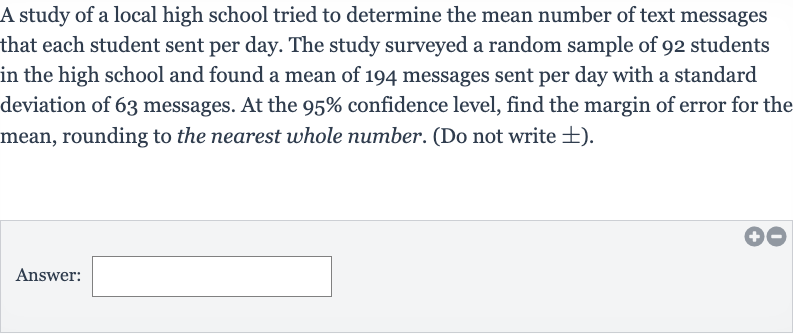
A study of a local high school tried to determine the mean number of text messages that each student sent per day. The study surveyed a random sample of 92 students in the high school and found a mean of 194 messages sent per day with a standard deviation of 63 messages. At the 95% confidence level, find the margin of error for the mean, rounding to the nearest whole number. (Do not write +- ). Answer:

A study of a local high school tried to determine the mean number of text messages that each student sent per day. The study surveyed a random sample of 9292 students in the high school and found a mean of 194194 messages sent per day with a standard deviation of 6363 messages. At the 95% 95 \% confidence level, find the margin of error for the mean, rounding to the nearest whole number. (Do not write ± \pm ).\newlineAnswer:

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 2right chevron icon
Interpret confidence intervals for population meansright chevron icon

Full solution

Q. A study of a local high school tried to determine the mean number of text messages that each student sent per day. The study surveyed a random sample of 9292 students in the high school and found a mean of 194194 messages sent per day with a standard deviation of 6363 messages. At the 95% 95 \% confidence level, find the margin of error for the mean, rounding to the nearest whole number. (Do not write ± \pm ).\newlineAnswer:
  1. Identify Formula: To find the margin of error at the 95%95\% confidence level, we need to use the formula for the margin of error (ME) in a sample mean, which is ME=z×(σ/n)ME = z \times (\sigma/\sqrt{n}), where zz is the z-score corresponding to the confidence level, σ\sigma is the standard deviation, and nn is the sample size.
  2. Find Z-Score: First, we need to find the z-score that corresponds to the 95%95\% confidence level. For a 95%95\% confidence interval, the z-score is typically 1.961.96 because it captures the central 95%95\% of the normal distribution.
  3. Calculate Margin of Error: Next, we will plug in the values for the standard deviation (σ=63\sigma = 63 messages) and the sample size (n=92n = 92 students) into the margin of error formula.
  4. Plug in Values: Now, we calculate the margin of error using the formula ME=z×(σ/n)=1.96×(63/92)ME = z \times (\sigma/\sqrt{n}) = 1.96 \times (63/\sqrt{92}).
  5. Calculate Square Root: We calculate the square root of the sample size, 92\sqrt{92}, which is approximately 9.59179.5917.
  6. Divide Standard Deviation: Now, we divide the standard deviation by the square root of the sample size: 639.5917≈6.5707\frac{63}{9.5917} \approx 6.5707.
  7. Multiply Z-Score: Finally, we multiply the z-score by this result to find the margin of error: 1.96×6.5707≈12.87861.96 \times 6.5707 \approx 12.8786.
  8. Round to Nearest Whole: Since we need to round to the nearest whole number, the margin of error is approximately 1313 messages.

More problems from Interpret confidence intervals for population means

Question
Michael surveyed 22 politicians from his state about their views on certain issues.\newlineIs this sample of citizens of the state likely to be biased?\newlineChoices:\newline[A]yes\newline[B]no
Get tutor helpright-arrow

Posted 7 months ago

Question
Read the following description of an experiment.\newlineA massage therapist has received complaints that the fragrance of her massage oil is unpleasant. She is testing whether a new oil will improve each clients' experience.\newlineThe massage therapist randomly sorts her clients into two groups. She massages 55 clients from the first group with the new oil and 55 from the other group with her usual oil. She asks all 1010 clients to rate their massages.\newlineIs this experiment statistically well designed?\newlineChoices:\newline[A]yes\newline[B]no
Get tutor helpright-arrow

Posted 7 months ago

Question
A random sample of 3535 four-door passenger vehicles had a mean gas mileage, in miles per gallon (mpg) (\mathrm{mpg}) , of 25.9mpg 25.9 \mathrm{mpg} . The estimate had a margin of error of 2.6mpg 2.6 \mathrm{mpg} at a 98% 98 \% confidence level. Of the following, which is the most plausible value for the true mean gas mileage of all four-door passenger vehicles?\newlineChoose 11 answer:\newline(A) 24mpg 24 \mathrm{mpg} \newline(B) 29mpg 29 \mathrm{mpg} \newline(C) 32mpg 32 \mathrm{mpg} \newline(D) 35mpg 35 \mathrm{mpg}
Get tutor helpright-arrow

Posted 8 months ago

Question
In a poll of 11,578578 randomly selected American adults, 44.8% 44.8 \% of the respondents said that airlines should allow in-flight calls on airplanes. The poll reported a margin of error of 2.5% 2.5 \% at a 95% 95 \% confidence level. Which of the following is most likely to be equal to the percentage of all American adults who would say that airlines should allow in-flight calls?\newlineChoose 11 answer:\newline(A) 40% 40 \% \newline(B) 43% 43 \% \newline(C) 48% 48 \% \newline(D) 95% 95 \%
Get tutor helpright-arrow

Posted 10 months ago

Question
Malik walked up and back down an empty 18 m 18 \mathrm{~m} long escalator at a constant rate. Since the escalator was going up at the time, it took him only 22.5 s 22.5 \mathrm{~s} . Going down took Malik 9090 s. Assume the escalator speed is constant.\newlineWhat was Malik's walking speed?\newlinems \frac{\mathrm{m}}{\mathrm{s}}
Get tutor helpright-arrow

Posted 8 months ago

Question
Two baseball players are warming up by throwing balls to the catcher. The two players are located 1010 yards apart, and the angle from each player to the catcher is 55∘55^{\circ} and 71∘71^{\circ}, respectively. What is the distance from the farthest baseball player to the catcher?\newlineA. 10.12510.125 yards\newlineB. 11.68711.687 yards\newlineC. 14.50114.501 yards\newlineD. 14.79014.790 yards
Get tutor helpright-arrow

Posted 8 months ago

Question
Select the outlier in the data set.\newline74,84,86,87,89,91,92,98,12674,84,86,87,89,91,92,98,126
Get tutor helpright-arrow

Posted 8 months ago

Question
Solve for p p .p8=79p=□\begin{array}{l}\frac{p}{8}=\frac{7}{9} \\p=\square\end{array}
Get tutor helpright-arrow

Posted 8 months ago

Question
Jelani needs to hire at least 1212 artists for an upcoming event. He needs to hire visual artists, who will be paid $300\$300 for the event, and performers, who will be paid $480\$480 for the event. His budget for paying the artists is no more than $6,000\$6,000. He must hire at least 44 visual artists and at least 33 performers. Which of the following does not satisfy all of the conditions described?\newlineChoose 11 answer:\newline(A) 44 visual artists and 1010 performers\newline(B) 88 visual artists and 88 performers\newline(C) $300\$30000 visual artists and 33 performers\newline(D) $300\$30022 visual artists and 44 performers
Get tutor helpright-arrow

Posted 8 months ago

Question
Factor.\newlinek2+9k+18k^2 + 9k + 18\newline____\newline
Get tutor helpright-arrow

Posted 8 months ago

View all (47)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant