Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

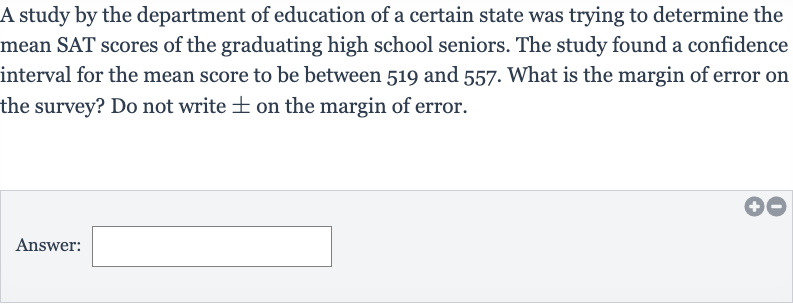
A study by the department of education of a certain state was trying to determine the mean SAT scores of the graduating high school seniors. The study found a confidence interval for the mean score to be between 519 and 557 . What is the margin of error on the survey? Do not write
+- on the margin of error.
Answer:____

A study by the department of education of a certain state was trying to determine the mean SAT scores of the graduating high school seniors. The study found a confidence interval for the mean score to be between $519$ and $557$ . What is the margin of error on the survey? Do not write $\pm$ on the margin of error. $\newline$ Answer:_______

View step-by-step help

View step-by-step help

Interpret confidence intervals for population means

Full solution

Q. A study by the department of education of a certain state was trying to determine the mean SAT scores of the graduating high school seniors. The study found a confidence interval for the mean score to be between

519

and

557

. What is the margin of error on the survey? Do not write

\pm

on the margin of error.

\newline

Answer:_______

Understand concept: Understand the concept of a confidence interval and margin of error. The confidence interval gives a range within which the true mean is expected to lie. The margin of error is the amount added to and subtracted from the point estimate (like the sample mean) to create the confidence interval.
Identify bounds: Identify the lower and upper bounds of the confidence interval. $\newline$ The confidence interval is given as between $519$ and $557$ . $\newline$ Lower bound = $519$ $\newline$ Upper bound = $557$
Calculate point estimate: Calculate the point estimate (mean) of the confidence interval. $\newline$ The point estimate is the midpoint of the confidence interval. $\newline$ Point estimate (mean) = $(\text{Lower bound} + \text{Upper bound}) / 2$ $\newline$ Point estimate (mean) = $(519 + 557) / 2$ $\newline$ Point estimate (mean) = $1076 / 2$ $\newline$ Point estimate (mean) = $538$
Calculate margin of error: Calculate the margin of error. $\newline$ The margin of error is the difference between the point estimate and one of the bounds of the confidence interval. $\newline$ Margin of error = Upper bound - Point estimate $\newline$ Margin of error = $557 - 538$ $\newline$ Margin of error = $19$

More problems from Interpret confidence intervals for population means

Question

Michael surveyed

2

politicians from his state about their views on certain issues.

\newline

Is this sample of citizens of the state likely to be biased?

\newline

\newline

\newline

Posted 1 month ago

Question

Read the following description of an experiment.

\newline

A massage therapist has received complaints that the fragrance of her massage oil is unpleasant. She is testing whether a new oil will improve each clients' experience.

\newline

The massage therapist randomly sorts her clients into two groups. She massages

5

clients from the first group with the new oil and

5

from the other group with her usual oil. She asks all

10

clients to rate their massages.

\newline

Is this experiment statistically well designed?

\newline

\newline

\newline

Posted 1 month ago

Question

A random sample of

35

four-door passenger vehicles had a mean gas mileage, in miles per gallon

(\mathrm{mpg})

25.9 \mathrm{mpg}

. The estimate had a margin of error of

2.6 \mathrm{mpg}

98 \%

confidence level. Of the following, which is the most plausible value for the true mean gas mileage of all four-door passenger vehicles?

\newline

1

\newline

24 \mathrm{mpg}

\newline

29 \mathrm{mpg}

\newline

32 \mathrm{mpg}

\newline

35 \mathrm{mpg}

Posted 2 months ago

Question

1

578

randomly selected American adults,

44.8 \%

of the respondents said that airlines should allow in-flight calls on airplanes. The poll reported a margin of error of

2.5 \%

95 \%

confidence level. Which of the following is most likely to be equal to the percentage of all American adults who would say that airlines should allow in-flight calls?

\newline

1

\newline

40 \%

\newline

43 \%

\newline

48 \%

\newline

95 \%

Posted 4 months ago

Question

Malik walked up and back down an empty

18 \mathrm{~m}

long escalator at a constant rate. Since the escalator was going up at the time, it took him only

22.5 \mathrm{~s}

. Going down took Malik

90

s. Assume the escalator speed is constant.

\newline

What was Malik's walking speed?

\newline

\frac{\mathrm{m}}{\mathrm{s}}

Posted 2 months ago

Question

Two baseball players are warming up by throwing balls to the catcher. The two players are located

10

yards apart, and the angle from each player to the catcher is

55^{\circ}

71^{\circ}

, respectively. What is the distance from the farthest baseball player to the catcher?

\newline

10.125

\newline

11.687

\newline

14.501

\newline

14.790

Posted 2 months ago

Question

Select the outlier in the data set.

\newline

74,84,86,87,89,91,92,98,126

Posted 2 months ago

Question

p

\begin{array}{l}\frac{p}{8}=\frac{7}{9} \\p=\square\end{array}

Posted 2 months ago

Question

Jelani needs to hire at least

12

artists for an upcoming event. He needs to hire visual artists, who will be paid

\$300

for the event, and performers, who will be paid

\$480

for the event. His budget for paying the artists is no more than

\$6,000

. He must hire at least

4

visual artists and at least

3

performers. Which of the following does not satisfy all of the conditions described?

\newline

1

\newline

4

visual artists and

10

\newline

8

visual artists and

8

\newline

\$300

0

visual artists and

3

\newline

\$300

2

visual artists and

4

Posted 1 month ago

Question

\newline

k^2 + 9k + 18

\newline

\newline

Posted 2 months ago