Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

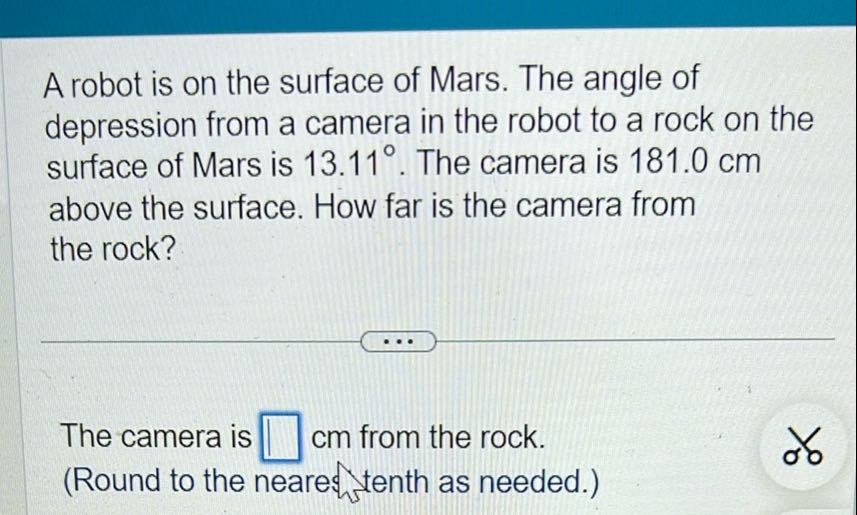
A robot is on the surface of Mars. The angle of depression from a camera in the robot to a rock on the surface of Mars is 13.11^(@). The camera is 181.0cm above the surface. How far is the camera from the rock? The camera is ◻ cm from the rock. (Round to the neare tenth as needed.)

A robot is on the surface of Mars. The angle of depression from a camera in the robot to a rock on the surface of Mars is 13.11∘ 13.11^{\circ} . The camera is 181.0 cm 181.0 \mathrm{~cm} above the surface. How far is the camera from the rock?\newlineThe camera is □ \square cm \mathrm{cm} from the rock.\newline(Round to the neare tenth as needed.)

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 2right chevron icon
Solve quadratic equations: word problemsright chevron icon

Full solution

Q. A robot is on the surface of Mars. The angle of depression from a camera in the robot to a rock on the surface of Mars is 13.11∘ 13.11^{\circ} . The camera is 181.0 cm 181.0 \mathrm{~cm} above the surface. How far is the camera from the rock?\newlineThe camera is □ \square cm \mathrm{cm} from the rock.\newline(Round to the neare tenth as needed.)
  1. Understand and Visualize: Understand the problem and visualize the scenario.\newlineWe are given the angle of depression from the camera to the rock, which is 13.1113.11 degrees. The camera is 181.0181.0 cm above the surface of Mars. We need to find the horizontal distance from the camera to the rock. This forms a right triangle with the angle of depression at the camera, the height of the camera as one leg, and the distance to the rock as the other leg.
  2. Convert to Elevation: Convert the angle of depression to the angle of elevation.\newlineThe angle of elevation from the base of the camera to the camera is equal to the angle of depression, which is 13.1113.11 degrees. This is because the angle of depression from the camera to the rock is congruent to the angle of elevation from the rock to the camera.
  3. Use Trigonometry: Use trigonometry to find the distance to the rock.\newlineWe can use the tangent of the angle of elevation to find the horizontal distance to the rock. The tangent of an angle in a right triangle is the ratio of the opposite side (height of the camera) to the adjacent side (distance to the rock).\newlineLet's denote the distance to the rock as dd. Then we have:\newlinetan⁡(13.11°)=oppositeadjacent\tan(13.11°) = \frac{\text{opposite}}{\text{adjacent}}\newlinetan⁡(13.11°)=181.0 cmd\tan(13.11°) = \frac{181.0\,\text{cm}}{d}
  4. Solve for Distance: Solve for the distance dd. To find dd, we rearrange the equation: d=181.0 cmtan⁡(13.11∘)d = \frac{181.0 \, \text{cm}}{\tan(13.11^\circ)} Now we calculate the value using a calculator. d≈181.0 cmtan⁡(13.11∘)d \approx \frac{181.0 \, \text{cm}}{\tan(13.11^\circ)} d≈181.0 cm0.232d \approx \frac{181.0 \, \text{cm}}{0.232} d≈780.172 cmd \approx 780.172 \, \text{cm}
  5. Round to Nearest Tenth: Round the distance to the nearest tenth. d≈780.2d \approx 780.2 cm

More problems from Solve quadratic equations: word problems

Question
Solve by completing the square.\newlinem2−10m−29=0m^2 - 10m - 29 = 0\newlineWrite your answers as integers, proper or improper fractions in simplest form, or decimals rounded to the nearest hundredth.\newline`m` = ____ or `m` = _____
Get tutor helpright-arrow

Posted 8 months ago

Question
Find g(x) g(x) , where g(x) g(x) is the translation 5 5 units up of f(x)=x2 f(x)=x^2 .\newlineWrite your answer in the form a(x–h)2+k a(x–h)^2+k , where a a , h h , and k k are integers.\newlineg(x)= g(x)= ____
Get tutor helpright-arrow

Posted 7 months ago

Question
What is the range of this quadratic function?\newliney=x2−4x+4y = x^2 - 4x + 4\newlineChoices:\newline{y∣y≥2}\left\{y \mid y \geq 2\right\}\newline{y∣y≤0}\left\{y \mid y \leq 0\right\}\newline{y∣y≥0}\left\{y \mid y \geq 0\right\}\newlineall real numbers\text{all real numbers}
Get tutor helpright-arrow

Posted 5 months ago

Question
Write the equation of the parabola that passes through the points (1,0)(1,0), (2,0)(2,0), and (3,–16)(3,\text{–}16). Write your answer in the form y=a(x–p)(x–q)y = a(x – p)(x – q), where aa, pp, and qq are integers, decimals, or simplified fractions.\newline______
Get tutor helpright-arrow

Posted 5 months ago

Question
Complete the square. Fill in the number that makes the polynomial a perfect-square quadratic.\newlinef2+8f+_____f^2 + 8f + \_\_\_\_\_
Get tutor helpright-arrow

Posted 5 months ago

Question
Solve for h h .\newlineh2+39h=0 h^2 + 39h = 0 \newline\newlineWrite each solution as an integer, proper fraction, or improper fraction in simplest form. If there are multiple solutions, separate them with commas.\newlineh= h = ____\newline
Get tutor helpright-arrow

Posted 5 months ago

Question
Write a quadratic function with zeros −9-9 and −7-7.\newlineWrite your answer using the variable xx and in standard form with a leading coefficient of 11.\newlinef(x)=_____f(x) = \_\_\_\_\_
Get tutor helpright-arrow

Posted 5 months ago

Question
Find the equation of the axis of symmetry for the parabola y=x2y = x^2. \newlineSimplify any numbers and write them as proper fractions, improper fractions, or integers.\newline‾\underline{\hspace{3cm}}
Get tutor helpright-arrow

Posted 4 months ago

Question
Find g(x)g(x), where g(x)g(x) is the translation 88 units up of f(x)=x2f(x) = x^2.\newlineWrite your answer in the form a(x–h)2+ka(x – h)^2 + k, where aa, hh, and kk are integers.\newlineg(x)=g(x) = ______\newline
Get tutor helpright-arrow

Posted 4 months ago

Question
Solve for xx.\newlinex2=1x^2 = 1\newline\newlineWrite your answer in simplified, rationalized form.\newlinex=x = ______ or x=x = ______\newline
Get tutor helpright-arrow

Posted 5 months ago

View all (79)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant