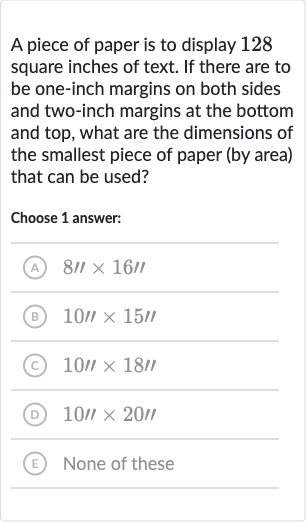
A piece of paper is to display $128$ square inches of text. If there are to be one-inch margins on both sides and two-inch margins at the bottom and top, what are the dimensions of the smallest piece of paper (by area) that can be used? $\newline$ Choose $1$ answer: $\newline$ (A) $8 \prime \prime \times 16 \prime \prime$ $\newline$ (B) $10 \prime \prime \times 15 \prime \prime$ $\newline$ (C) $10 \prime \prime \times 18 \prime \prime$ $\newline$ (D) $10 \prime \prime \times 20 \prime \prime$ $\newline$ (E) None of these

View step-by-step help

Home

Math Problems

Algebra 1

Transformations of functions

Full solution

Q. A piece of paper is to display

128

square inches of text. If there are to be one-inch margins on both sides and two-inch margins at the bottom and top, what are the dimensions of the smallest piece of paper (by area) that can be used?

\newline

Choose

1

answer:

\newline

(A)

8 \prime \prime \times 16 \prime \prime

\newline

(B)

10 \prime \prime \times 15 \prime \prime

\newline

(C)

10 \prime \prime \times 18 \prime \prime

\newline

(D)

10 \prime \prime \times 20 \prime \prime

\newline

(E) None of these

Define Variables: Let's call the width of the paper $x$ inches and the height $y$ inches. The text area is $128$ square inches.
Calculate Text Area: Since there are $1$ -inch margins on both sides, the text width is $x - 2$ inches.
Solve for Text Height: And since there are two-inch margins at the bottom and top, the text height is $y - 4$ inches.
Minimize Paper Area: The area for the text is $(x - 2)(y - 4) = 128$ square inches.
Evaluate Option (A): Now we solve for one variable in terms of the other. Let's solve for $y$ : $y = \frac{128}{(x - 2)} + 4$ .
Evaluate Option (B): To minimize the area of the paper, we want the smallest difference between $x$ and $y$ , ideally making $x = y$ for a square shape, which is the most area-efficient. But since we have different margins, we can't have a square.
Evaluate Option (C): We need to find the smallest integer values of $x$ and $y$ that satisfy the equation and the condition that the text area is $128$ square inches. Let's try the options given.
Evaluate Option (D): Option (A): $8\times16$ . The text area would be $(8 - 2)(16 - 4) = 6\times12 = 72$ square inches. This is not enough.
Final Answer: Option (B): $10\times15$ . The text area would be $(10 - 2)(15 - 4) = 8\times11 = 88$ square inches. This is also not enough.
Final Answer: Option (B): $10\times15$ . The text area would be $(10 - 2)(15 - 4) = 8\times11 = 88$ square inches. This is also not enough.Option (C): $10\times18$ . The text area would be $(10 - 2)(18 - 4) = 8\times14 = 112$ square inches. Still not enough.
Final Answer: Option (B): $10＂\times15＂$ . The text area would be $(10 - 2)(15 - 4) = 8\times11 = 88$ square inches. This is also not enough.Option (C): $10＂\times18＂$ . The text area would be $(10 - 2)(18 - 4) = 8\times14 = 112$ square inches. Still not enough.Option (D): $10＂\times20＂$ . The text area would be $(10 - 2)(20 - 4) = 8\times16 = 128$ square inches. This is correct, but let's check if it's the smallest.
Final Answer: Option (B): $10＂\times15＂$ . The text area would be $(10 - 2)(15 - 4) = 8\times11 = 88$ square inches. This is also not enough.Option (C): $10＂\times18＂$ . The text area would be $(10 - 2)(18 - 4) = 8\times14 = 112$ square inches. Still not enough.Option (D): $10＂\times20＂$ . The text area would be $(10 - 2)(20 - 4) = 8\times16 = 128$ square inches. This is correct, but let's check if it's the smallest.We don't have any other options that are smaller than $10＂\times20＂$ that can still fit the $128$ square inches of text, so option (D) is the smallest possible paper size.