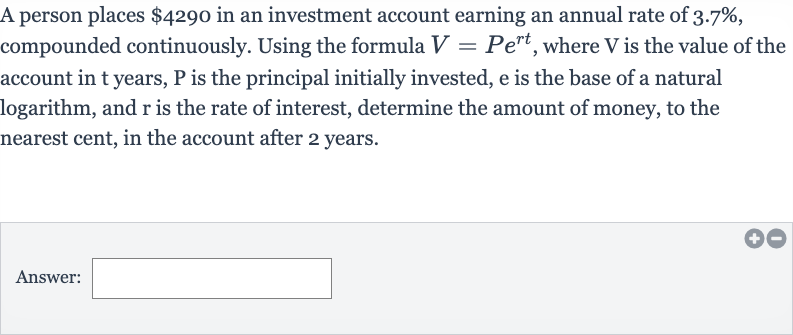
A person places $4290 in an investment account earning an annual rate of 3.7%, compounded continuously. Using the formula V=Pe^(rt), where V is the value of the account in t years, P is the principal initially invested, e is the base of a natural logarithm, and r is the rate of interest, determine the amount of money, to the nearest cent, in the account after 2 years. Answer:

Question

A person places  $4290 in an investment account earning an annual rate of  3.7%, compounded continuously. Using the formula  V=Pe^(rt), where  V is the value of the account in  t years,  P is the principal initially invested,  e is the base of a natural logarithm, and  r is the rate of interest, determine the amount of money, to the nearest cent, in the account after 2 years. Answer:

Bytelearn · Accepted Answer

Identify Given Values: Identify the given values from the problem. Principal (P) = $4290 Rate of interest (r) = 3.7% or 0.037 (as a decimal) Time (t) = 2 years We will use the formula V = Pe^(rt) to find the value of the account after 2 years.Convert to Decimal: Convert the percentage rate to a decimal. To convert a percentage to a decimal, divide by 100. 3.7% = 3.7 / 100 = 0.037Substitute into Formula: Substitute the values into the formula. V = 4290 * e^(0.037 * 2)Calculate Exponent: Calculate the exponent part of the formula. 0.037 * 2 = 0.074Calculate e Value: Calculate e raised to the power of the exponent. e^0.074 (Use a calculator for this step) e^0.074 ≈ 1.076849Multiply Principal: Multiply the principal by the result from the previous step. V = 4290 * 1.076849Find Account Value: Perform the multiplication to find the value of the account after 2 years. V ≈ 4290 * 1.076849 ≈ 4620.03

Full solution

More problems from Compound interest

Related topics