Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

A hyperbola centered at the origin has vertices at
(+-sqrt61,0) and foci at
(+-sqrt98,0).
Write the equation of this hyperbola.

A hyperbola centered at the origin has vertices at $( \pm \sqrt{61}, 0)$ and foci at $( \pm \sqrt{98}, 0)$ . $\newline$ Write the equation of this hyperbola.

View step-by-step help

View step-by-step help

Write equations of hyperbolas in standard form using properties

Full solution

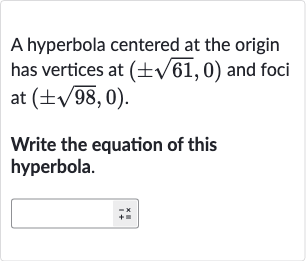
Q. A hyperbola centered at the origin has vertices at

( \pm \sqrt{61}, 0)

and foci at

( \pm \sqrt{98}, 0)

.

\newline

Write the equation of this hyperbola.

Identify standard form: Identify the standard form of the equation for a hyperbola centered at the origin with horizontal transverse axis. $\newline$ Standard form of equation for a hyperbola with horizontal transverse axis: $\newline$ $(\frac{x^2}{a^2}) - (\frac{y^2}{b^2}) = 1$
Determine values of $a$ and $a^2$ : Determine the values of $a$ and $a^2$ . The vertices are at $(\pm\sqrt{61},0)$ , so $a = \sqrt{61}$ and $a^2 = 61$ .
Determine values of $c$ and $c^2$ : Determine the values of $c$ and $c^2$ . The foci are at $(\pm\sqrt{98},0)$ , so $c = \sqrt{98}$ and $c^2 = 98$ .
Use relationship $c^2 = a^2 + b^2$ : Use the relationship $c^2 = a^2 + b^2$ to find $b^2$ . Substitute the known values of $a^2$ and $c^2$ into the equation. $98 = 61 + b^2$ $b^2 = 98 - 61$ $b^2 = 37$
Write equation in standard form: Write the equation of the hyperbola in standard form using the values of $a^2$ and $b^2$ . $\newline$ Substitute $a^2 = 61$ and $b^2 = 37$ into the standard form equation $(x^2/a^2) - (y^2/b^2) = 1$ . $\newline$ $(x^2/61) - (y^2/37) = 1$

More problems from Write equations of hyperbolas in standard form using properties

Question

Write the equation in standard form for the hyperbola

x^2 - y^2 = 64

\newline

Posted 3 months ago

Question

What is the center of the hyperbola

4x^2 - y^2 - 100 = 0

\newline

(\_,\_)

Posted 3 months ago

Question

What is the center of the hyperbola

(\frac{x^2}{144}) - (\frac{y^2}{81}) = 1

\newline

Posted 3 months ago

Question

What is the length of the transverse axis of the hyperbola

(\frac{x^2}{64}) - (\frac{y^2}{36}) = 1

\newline

Posted 3 months ago

Question

Write the equation in standard form for the hyperbola

y^2 - x^2 = 81

\newline

Posted 4 months ago

Question

Write the equation in standard form for the hyperbola

x^2 - 4y^2 = 100

\newline

Posted 4 months ago

Question

Write the equation in standard form for the hyperbola

9y^2 - x^2 = 36

\newline

Posted 4 months ago

Question

Write the equation in standard form for the hyperbola

4x^2 - y^2 = 16

\newline

Posted 4 months ago

Question

Write the equation in standard form for the hyperbola

y^2 - 9x^2 = 144

\newline

Posted 4 months ago

Question

y=f(x+3)

is shown. For which value of

x

, rounded to the nearest whole number, must

f(x)=0

Posted 1 month ago