Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

A hyperbola centered at the origin has vertices at
(0,+-sqrt12) and foci at
(0,+-sqrt45).
Write the equation of this hyperbola.

A hyperbola centered at the origin has vertices at $(0, \pm \sqrt{12})$ and foci at $(0, \pm \sqrt{45})$ . $\newline$ Write the equation of this hyperbola.

View step-by-step help

View step-by-step help

Write equations of hyperbolas in standard form using properties

Full solution

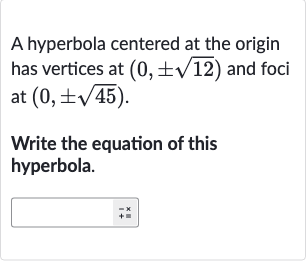
Q. A hyperbola centered at the origin has vertices at

(0, \pm \sqrt{12})

and foci at

(0, \pm \sqrt{45})

.

\newline

Write the equation of this hyperbola.

Standard Form of Hyperbola Equation: Identify the standard form of the equation for a hyperbola centered at the origin with a vertical transverse axis. $\newline$ Standard form of equation for a hyperbola with vertical transverse axis: $\newline$ $(y-k)^2/a^2 - (x-h)^2/b^2 = 1$ where $(h, k)$ is the center of the hyperbola.
Determining the Center: Determine the center $(h, k)$ of the hyperbola. Since the hyperbola is centered at the origin, we have $h = 0$ and $k = 0$ .
Finding the Semi-Major Axis: Find the value of the semi-major axis $a$ . The vertices are given at $(0, \pm\sqrt{12})$ , so the distance from the center to a vertex is $\sqrt{12}$ . Therefore, $a = \sqrt{12}$ .
Finding the Semi-Minor Axis: Find the value of the semi-minor axis $b$ using the relationship $c^2 = a^2 + b^2$ , where $c$ is the distance from the center to a focus. $\newline$ The foci are given at $(0, \pm\sqrt{45})$ , so $c = \sqrt{45}$ . We already know that $a = \sqrt{12}$ . We can now solve for $b$ . $\newline$ $c^2 = a^2 + b^2$ $\newline$ $(\sqrt{45})^2 = (\sqrt{12})^2 + b^2$ $\newline$ $45 = 12 + b^2$ $\newline$ $c^2 = a^2 + b^2$ $0$ $\newline$ $c^2 = a^2 + b^2$ $1$ $\newline$ $c^2 = a^2 + b^2$ $2$
Writing the Equation in Standard Form: Write the equation of the hyperbola in standard form after substituting the values of $h$ , $k$ , $a$ , and $b$ . Substitute $h = 0$ , $k = 0$ , $a = \sqrt{12}$ , and $b = \sqrt{33}$ into the standard form equation $(y-k)^2/a^2 - (x-h)^2/b^2 = 1$ . $(y - 0)^2/(\sqrt{12})^2 - (x - 0)^2/(\sqrt{33})^2 = 1$ $k$ $0$

More problems from Write equations of hyperbolas in standard form using properties

Question

Write the equation in standard form for the hyperbola

x^2 - y^2 = 64

\newline

Posted 2 months ago

Question

What is the center of the hyperbola

4x^2 - y^2 - 100 = 0

\newline

(\_,\_)

Posted 2 months ago

Question

What is the center of the hyperbola

(\frac{x^2}{144}) - (\frac{y^2}{81}) = 1

\newline

Posted 2 months ago

Question

What is the length of the transverse axis of the hyperbola

(\frac{x^2}{64}) - (\frac{y^2}{36}) = 1

\newline

Posted 2 months ago

Question

Write the equation in standard form for the hyperbola

y^2 - x^2 = 81

\newline

Posted 3 months ago

Question

Write the equation in standard form for the hyperbola

x^2 - 4y^2 = 100

\newline

Posted 3 months ago

Question

Write the equation in standard form for the hyperbola

9y^2 - x^2 = 36

\newline

Posted 3 months ago

Question

Write the equation in standard form for the hyperbola

4x^2 - y^2 = 16

\newline

Posted 3 months ago

Question

Write the equation in standard form for the hyperbola

y^2 - 9x^2 = 144

\newline

Posted 3 months ago

Question

y=f(x+3)

is shown. For which value of

x

, rounded to the nearest whole number, must

f(x)=0

Posted 25 days ago