Full solution
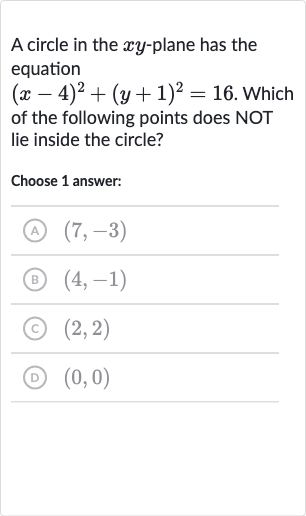
Q. A circle in the -plane has the equation. Which of the following points does NOT lie inside the circle?Choose answer:(A) (B) (C) (D)
- Circle Equation Explanation: The equation of the circle is given by . The center of the circle is at the point and the radius is the square root of , which is .
- Point Inside Circle Check: To determine if a point lies inside the circle, we can plug the coordinates of the point into the circle's equation and see if the resulting value is less than . If it is, the point lies inside the circle; if it is equal to , the point lies on the circle; and if it is greater than , the point lies outside the circle.
- Point A Check: Let's check point . Substitute and into the circle's equation: . Since is less than , point lies inside the circle.
- Point B Check: Now let's check point . Substitute and into the circle's equation: . Since is less than , point lies inside the circle.
- Point C Check: Next, let's check point . Substitute and into the circle's equation: . Since is less than , point lies inside the circle.
- Point D Check: Finally, let's check point (D) . Substitute and into the circle's equation: . Since is greater than , point (D) does NOT lie inside the circle.
More problems from Write a quadratic function from its x-intercepts and another point
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help